数据库笔记

过！过！过！

复习要点

绪论

文件系统vs数据库系统的特点

数据模型三个要素，层次模型，网状模型，关系模型的数据结构（zxs说前俩都没讲）

三级模式，二级映像，数据独立性

关系模型

三类完整性，主码和外码，参照关系被参照关系，参照完整性

关系代数基本运算必考！并差积……等等运算，唯独除法没出过！

SQL

明确指出不考触发器、断言

查询修改权限 sql有关的 20%

特点

create alter drop insert delete update select

单表多表查询

like，下划线，escape

sql一定有！

数据库安全性

明确指出不单考，完整性也不单考，放在sql里头

grant revoke语句

role

权限转授

自主存取控制和强制存取控制的概念

完整性

存在感不是很大

三类完整性的概念和实现

实体完整性 参照完整性很有可能考 自定义完整性

pk fk check unique not null

关系数据理论

35%

明确指出不考最小覆盖、正则覆盖。

明确指出不需要判断无损连接，但是要知道分解应该满足无损连接

明确指出从来只考基本，例如闭包计算，范式级别判断，找主码

从来没考过难题，简单的一塌糊涂

属性集闭包很有可能考，因为太简单，注重过程！！！比如循环一遍发现没有变化之类的

函数依赖公理系统

主码和找主码的过程

判断函数依赖是否成立

各个范式的判断

模式分解，分解算法都只是了解

数据库的设计 15%

必考

概念设计 er图

逻辑设计模式外模式

物理设计索引聚簇索引普通索引

重点是er转关系模式

代数优化

明确指出物理优化不会单考，可能顺带问一下怎么提高某个连接查询的性能

常用变换规则，各种启发式规则，反正就是那一套

连接规则

恢复

重点考系统故障，并且是带检查点的系统故障恢复，极有可能考

其他两个一个简单一个难，，，

并发控制

明确指出多粒度封锁不考

并发和恢复 20%

并发操作引起的数据不一致性

封锁和封锁协议

三级封锁协议，两段锁协议

死锁，预防死锁

可串行化，冲突可串行

可能要构造各种犀利把少的情况，也可能指定锁协议

必须用表格画，每一行必须只有一条语句

第八章存储引擎

明确指出只考槽页，估计八分

绪论

数据库管理系统（Database Management System-DBMS）是位于用户与操作系统之间的一层数据管理软件。MySQL等。

数据库系统DBS包括数据库DB、DBMS、数据库管理员DBA……

文件系统与数据库系统的区别

文件系统的数据是面向某一应用的，共享性差、冗余大，独立性差，文件内部的记录虽然是有结构的，但是整体无结构，由应用程序自己控制数据。
数据库系统中的数据不再仅仅面向某一个应用，而是面向所有用户。数据的共享性高、冗余度小，具有高度的物理独立性和逻辑独立性。数据库中的数据用数据模型组织和描述，由专门的软件DBMS提供安全性、完整性、并发控制和恢复能力。

二者的联系：

二者都是计算机系统中管理数据的软件。
文件系统是操作系统的重要组织部分，而DBMS是独立于操作系统的软件。DBMS 是在操作系统的基础上实现的，数据库中数据的组织和存储是通过操作系统中文件系统来实现的，数据库最终以文件的形式存在。DBMS对数据库的任何操作最终要转化为对文件的操作。

https://mooc1.chaoxing.com/mooc2/work/view?courseId=223830769&classId=53499154&cpi=114412111&workId=19336108&answerId=51506324&enc=405bce4e6721f80b22747108fc720834

层次模型，网状模型，关系模型

层次模型：

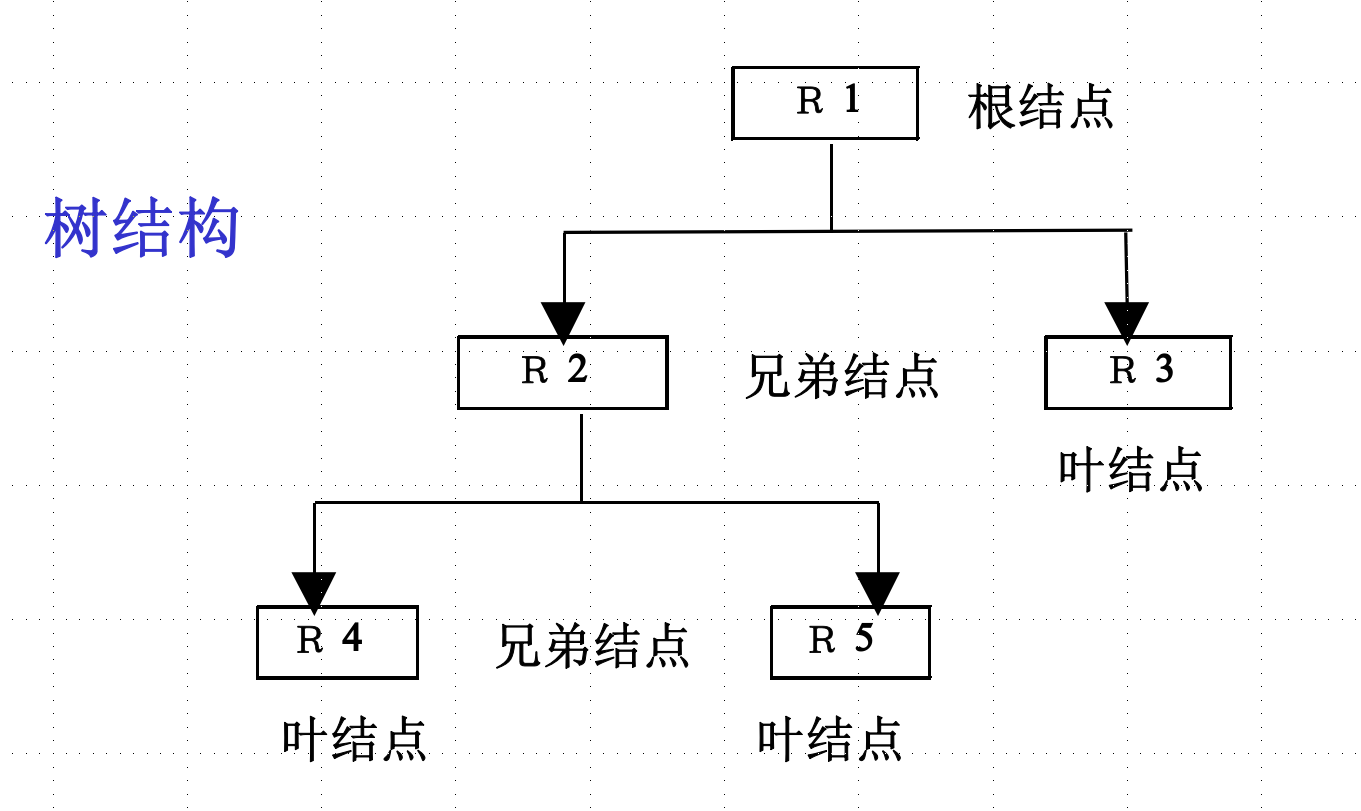
网状模型：（相比于树，允许无双亲和多个双亲）

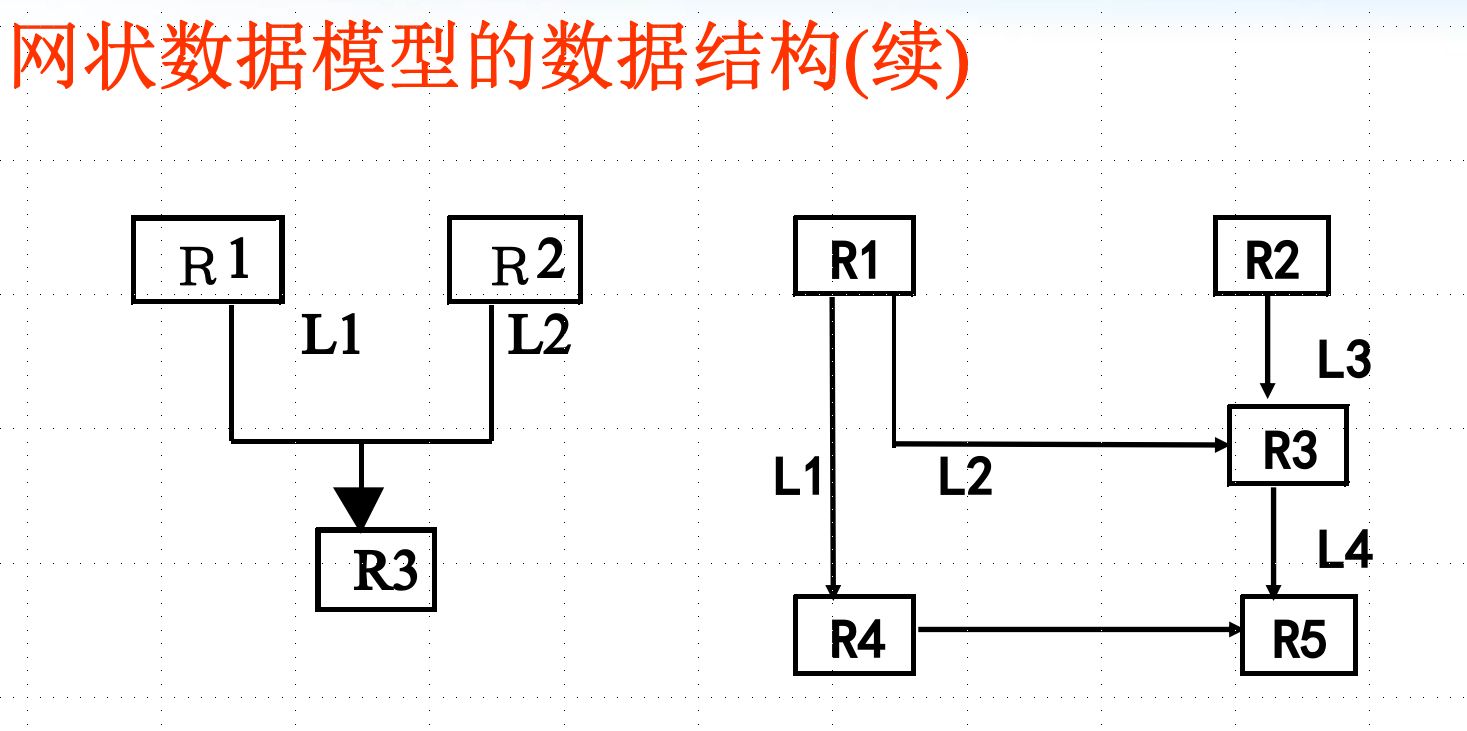
关系模型

关系模型中数据的逻辑结构是一张二维表，它由行和列组成。列表示属性，表间的特定冗余列信息表示实体间的联系

三级模式，二级映像，数据独立性

模式Schema是型的描述，不涉及具体的值，反映的是数据的结构及其联系，是相对稳定的

三级模式和二级映像：

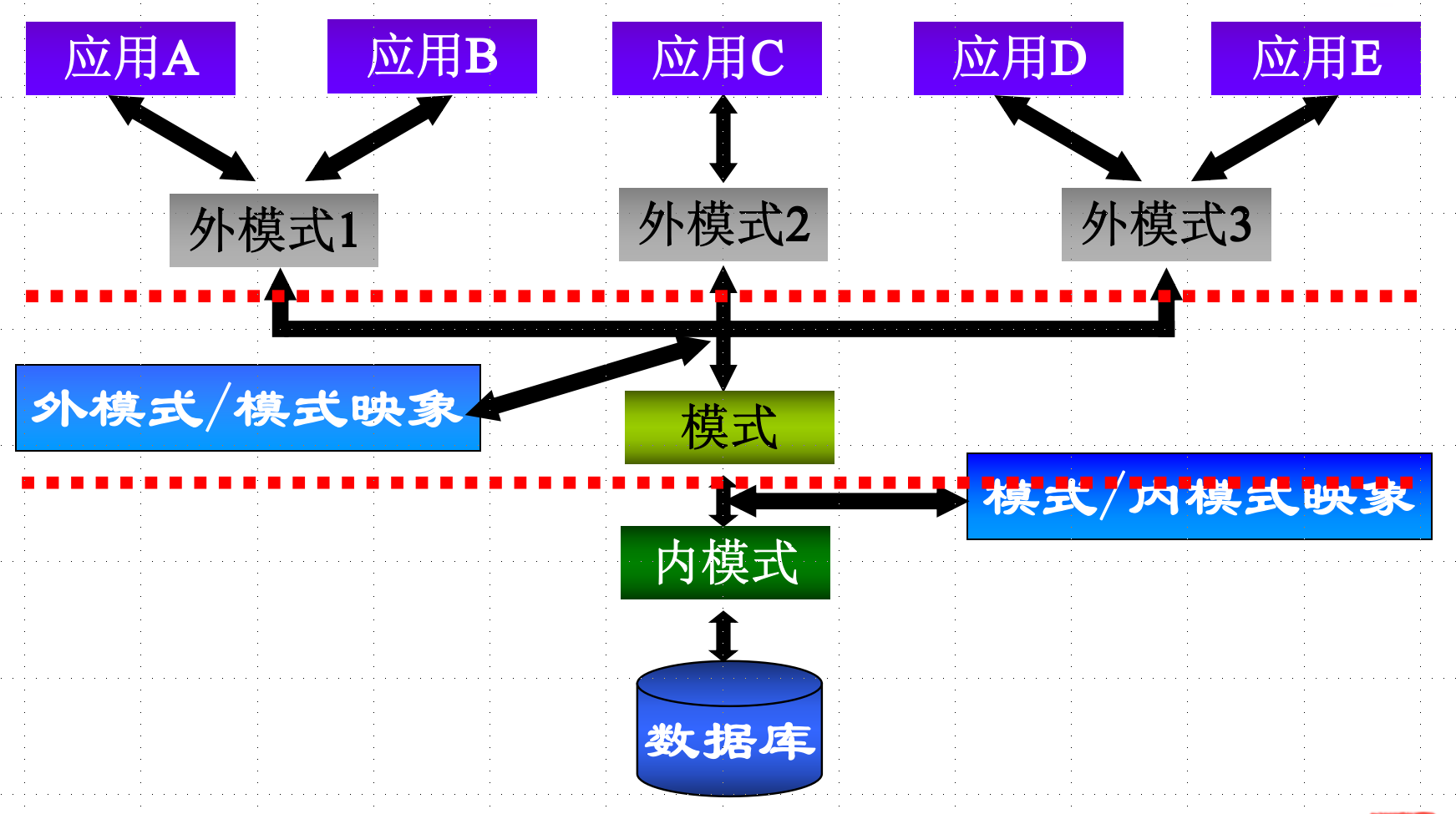
模式Schema，数据库中全体数据的逻辑结构和特征的描述。一个数据库只有一个模式，与数据的物理存储细节和硬件环境无关，与具体的应用程序、开发工具及高级程序设计语言无关.

外模式External Schema，数据库用户使用的局部数据的逻辑结构和特征的描述。一个数据库可能对应有多个外模式。

内模式Internal Schema，数据物理结构和存储方式的描述，一个数据库也只有一个内模式。

当模式改变时，数据库管理员修改有关的外模式／模式映象，使外模式保持不变
应用程序是依据数据的外模式编写的，从而应用程序不必修改，保证了数据与程序的逻辑独立性，简称数据的逻辑独立性。

当数据库的存储结构改变了（例如选用了另一种存储结构），数据库管理员修改模式／内模式映象，使模式保持不变
应用程序不受影响。保证了数据与程序的物理独立性，简称数据的物理独立性

数据模型，数据库系统的结构和组成

ER图：

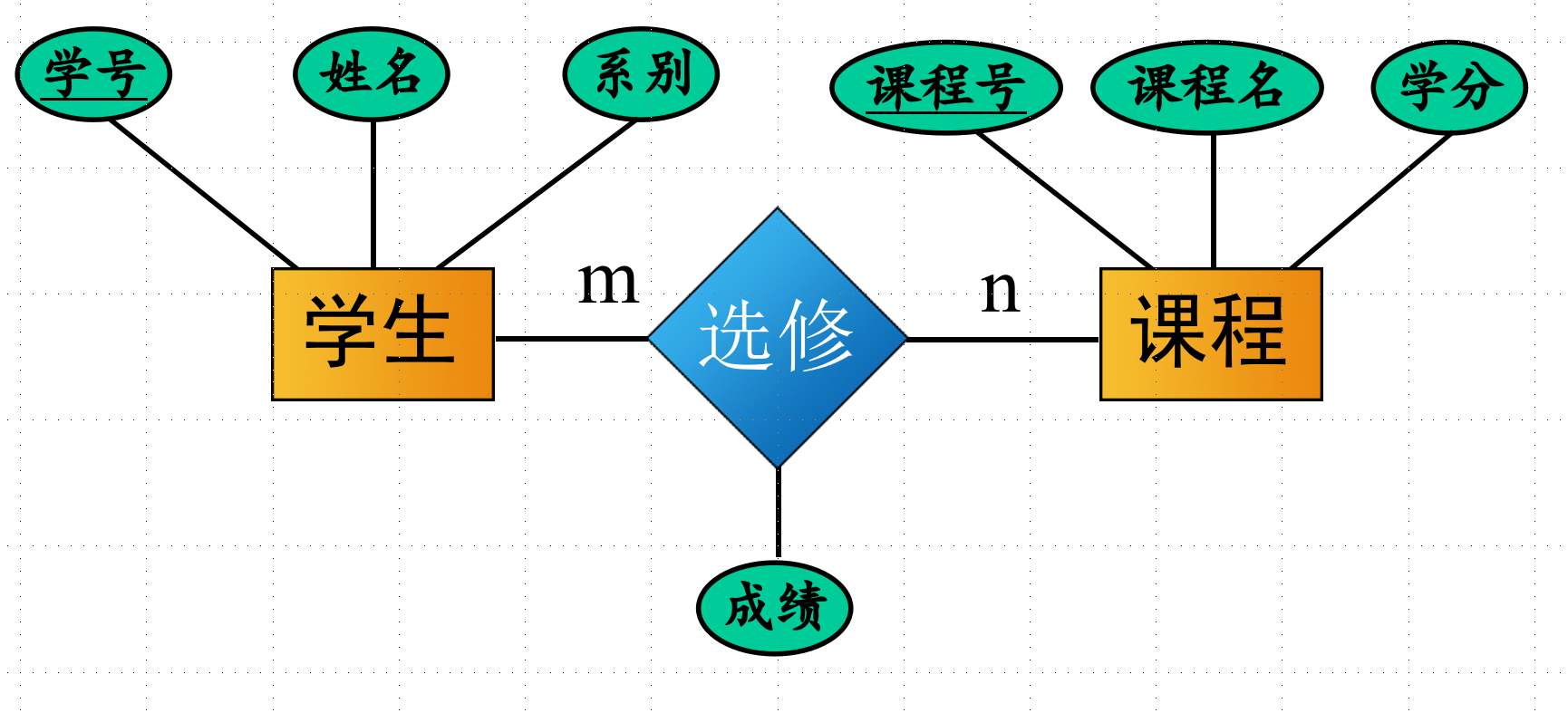
关系：对应通常说的一张表。

元组：表中的一行即为一个元组。

属性：表中的一列即为一个属性，给每一个属性起一个名称即属性名。

主码（Key）：表中的某个属性组，它可以唯一确定一个元组。

域（Domain）：属性的取值范围。

分量：元组中的一个属性值。

关系模式：对关系的描述，学生（学号，姓名，年龄，性别，系，年级）

关系数据库

三类关系，三类完整性

三类关系：基本关系（实际存在的）、查询表、视图表。

实体完整性：所有主属性不能取空值。

参照完整性：参照关系R，被参照关系S，R的一组属性F和S的主码$K_s$对应，则F为R的外码。则R中每个元组在F上的值要么为空值，要么等于S中某个元组的主码值。

用户定义的完整性。

关系数据结构

域、笛卡尔积顾名思义。笛卡尔积中每一个元素$(d_1,d_2,\ldots,d_n)$称为元组，其中$d_i$称为分量。

笛卡尔积的基数是所有域的大小的乘积。

关系是笛卡尔积的子集。$R(D1,D2,\ldots,Dn)$，R为关系名，n为关系的目/度。

总之，关系是一个二维表。

若关系中的某一属性组的值能唯一地标识一个元组，且去掉这组属性中的任何属性或属性组都不能唯一标识元组，则称该属性组为候选码。候选码的诸属性称为主属性，不包含在任何侯选码中的属性称为非码属性。

若一个关系有多个候选码，则选定其中一个为主码（Primary key）

关系R的属性组，跟与R联系的另一关系S中的码相对应，则称这个属性组为外码。

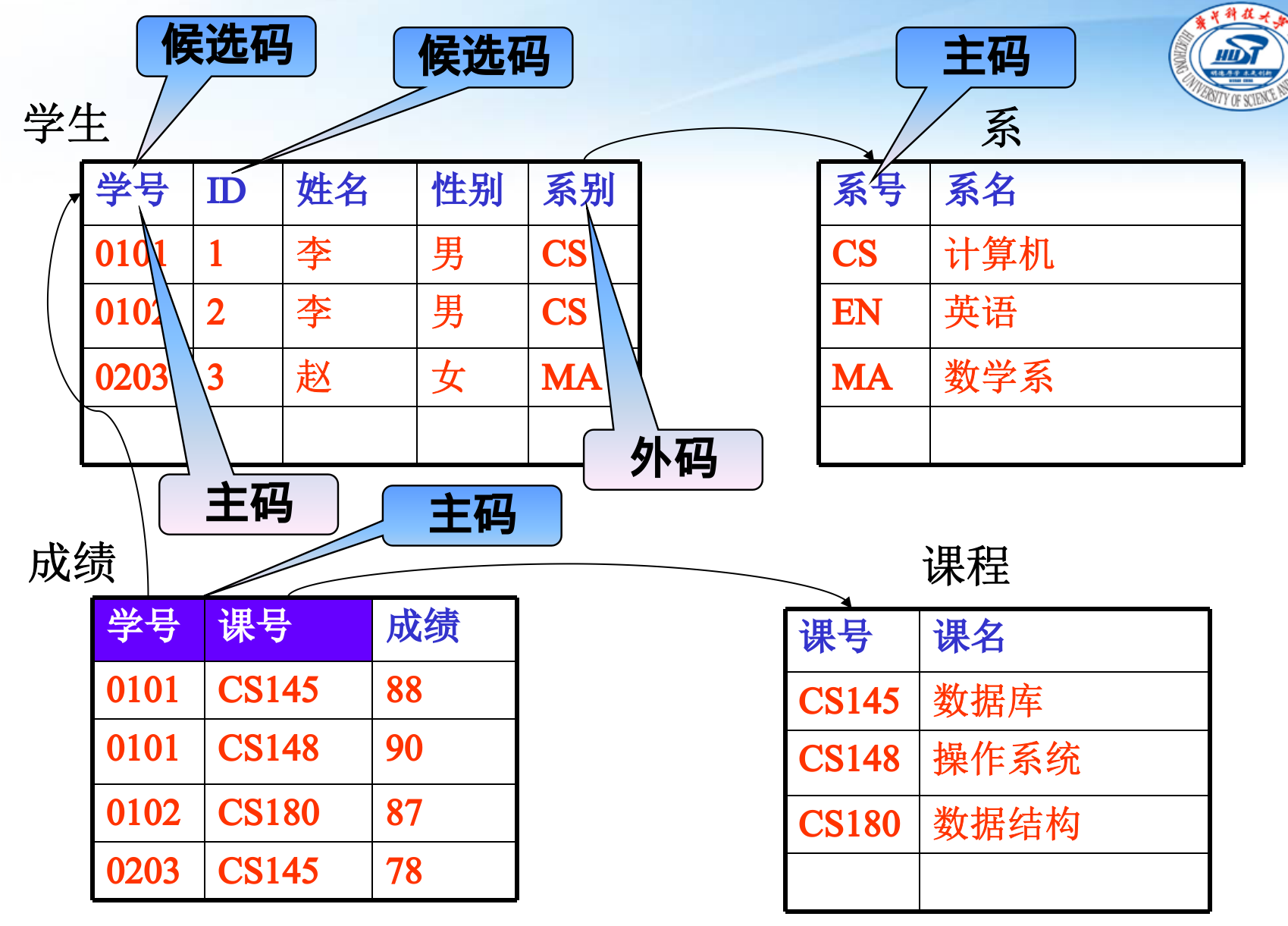
关系代数

分量和象集

若记t是R的一个元组，$t[A_i]$是t在属性$A_i$上的分量，A是属性们中的一部分，$t[A]$表示元组t在属性组A上的分量的集合，$\bar A$表示去掉A的k属性组。

象集表示关系R中属性组X上值为x的诸元组在属性组Z上分量的集合。（简单来说就是选择）。象集一般用$A_{b}$表示，用下面的投影表示就是$\Pi_{A}(\sigma_{B=b}(R))$。

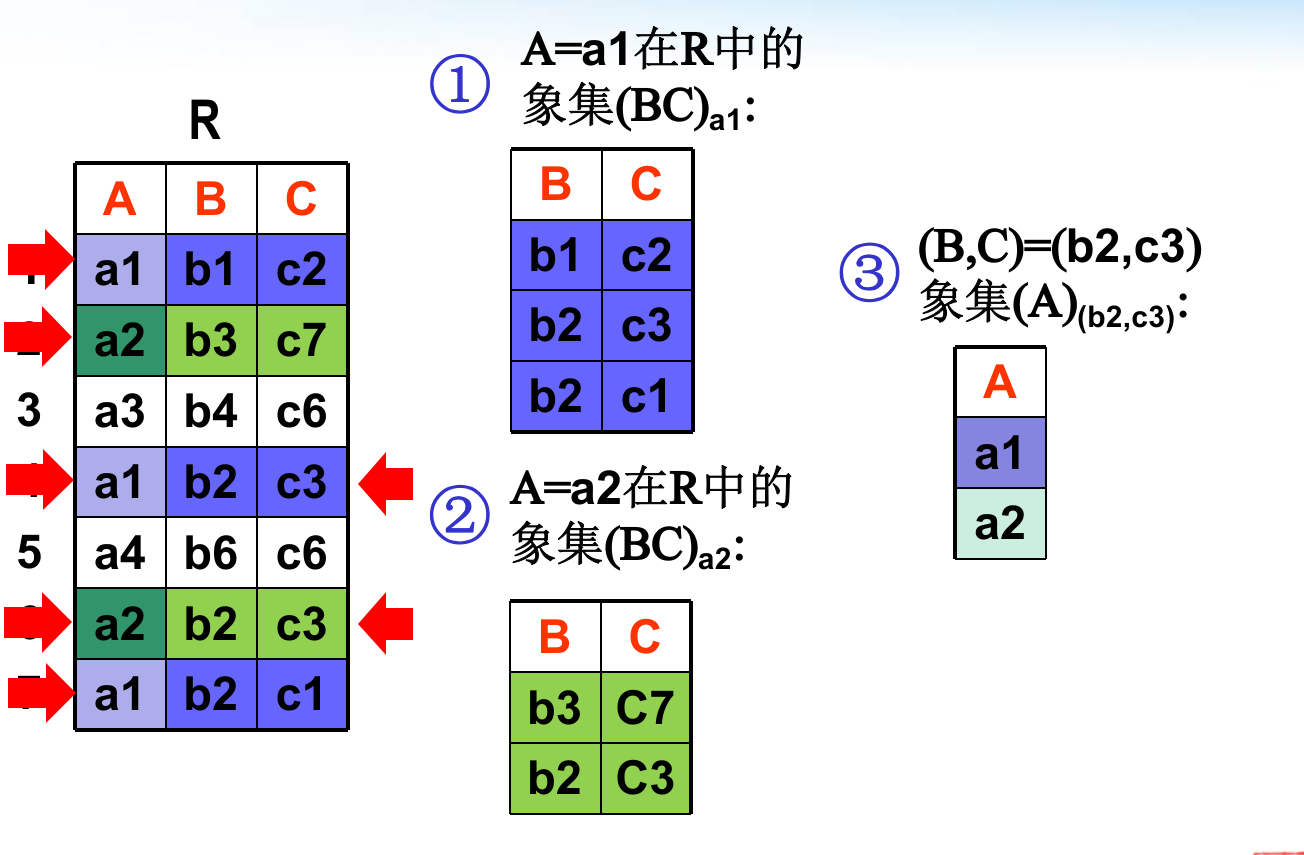
元组连接：$\overset{\frown} {t_rt_s}$

关系运算

运算对象和结果都是关系。因此结果一定是表!!!

基本的关系运算：并、差、笛卡尔积、选择、投影

选择：$\sigma_F (R) = {t|t\in R \and F(t)为真}$。自然是满足结合率啥的的。

投影：$\Pi_A(R) = { t[A] | t \in R } , A\subseteq U$，从R(U)中选出若干属性列组成新的关系。结果中要去掉相同行。

扩展的关系运算：交，连接，除

交：$R∩S = R - (R - S）= S - (S - R)$

除：R (X，Y) ÷S (Y，Z)， X，Y，Z为属性组，Z不重要。R.Y 与 S.Y 同语义 (可以不同名)。某种意义上可以把除法理解成整除。

$R÷S = {t [X] | t \in R \and \Pi_Y (S) \subseteq Y_{t[X]}}= \Pi_X(R) - \Pi_X(\Pi_X(R) \times \Pi_Y(S) - R)$.

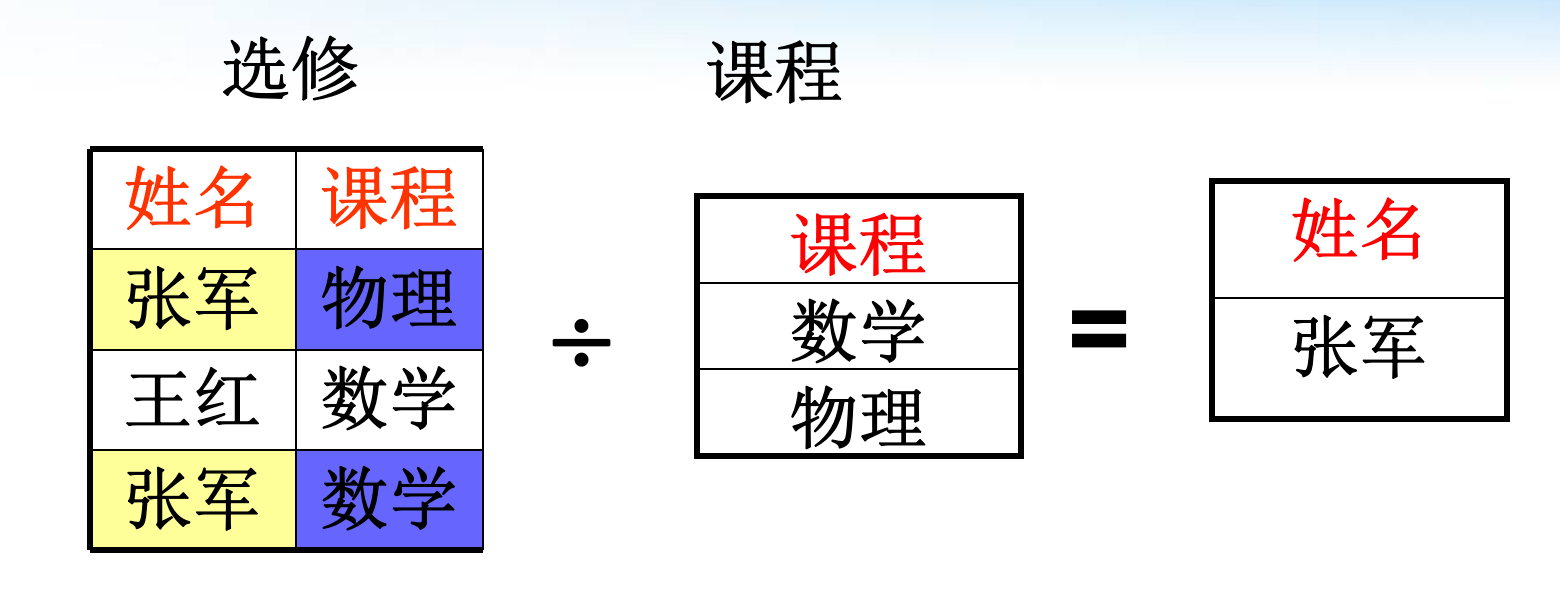
θ连接：R和S的笛卡尔积中选取R关系在A属性组上的值与S关系在B属性组上值满足θ比较关系的元组。广义定义$R \underset{A\theta B}{\Join} S = {\overset{\frown} {t_rt_s} |t_r \in R \and t_s\in S \and t_r[A]θt_s[B] }=\sigma_{R[A]θS[B]}( R×S)$，其中θ是一个运算符。

显然地，有一种等值连接，是从笛卡尔积中取得A、B属性值相等的那些元素。$R \underset{A= B}{\Join} S$。还有自然连接，是一种特殊的等值连接，比较的分量必须是相同属性组，在结果中要把重复的属性列去掉。$R(U_r)$和$S(U_s)$具有相同的属性组$B=U_r\cap U_s$ , $U=U_r\cup U_s$，$R \Join S = {\overset{\frown} {t_rt_s}[U] |t_r \in R \and t_s\in S \and t_r[B]=t_s[B] }$.

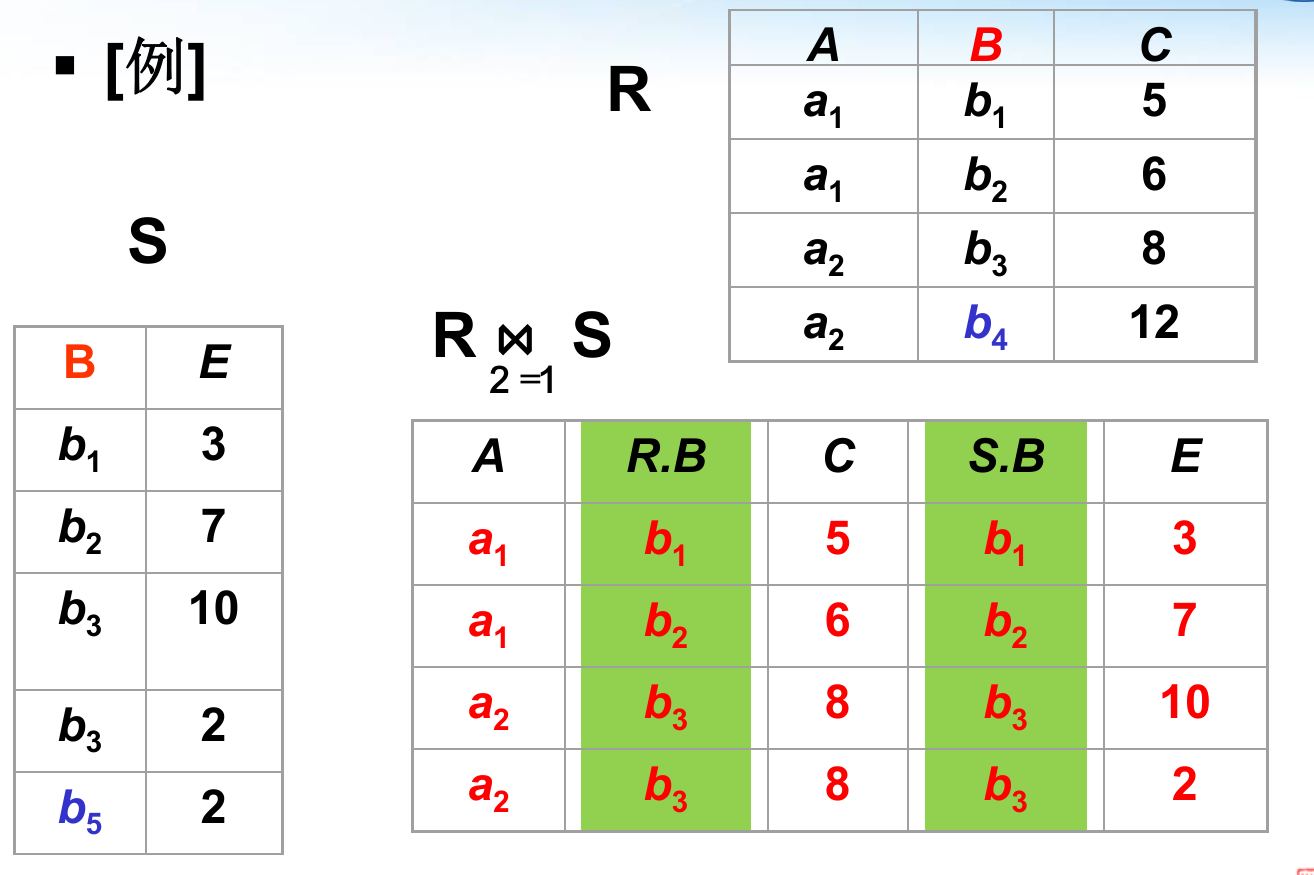
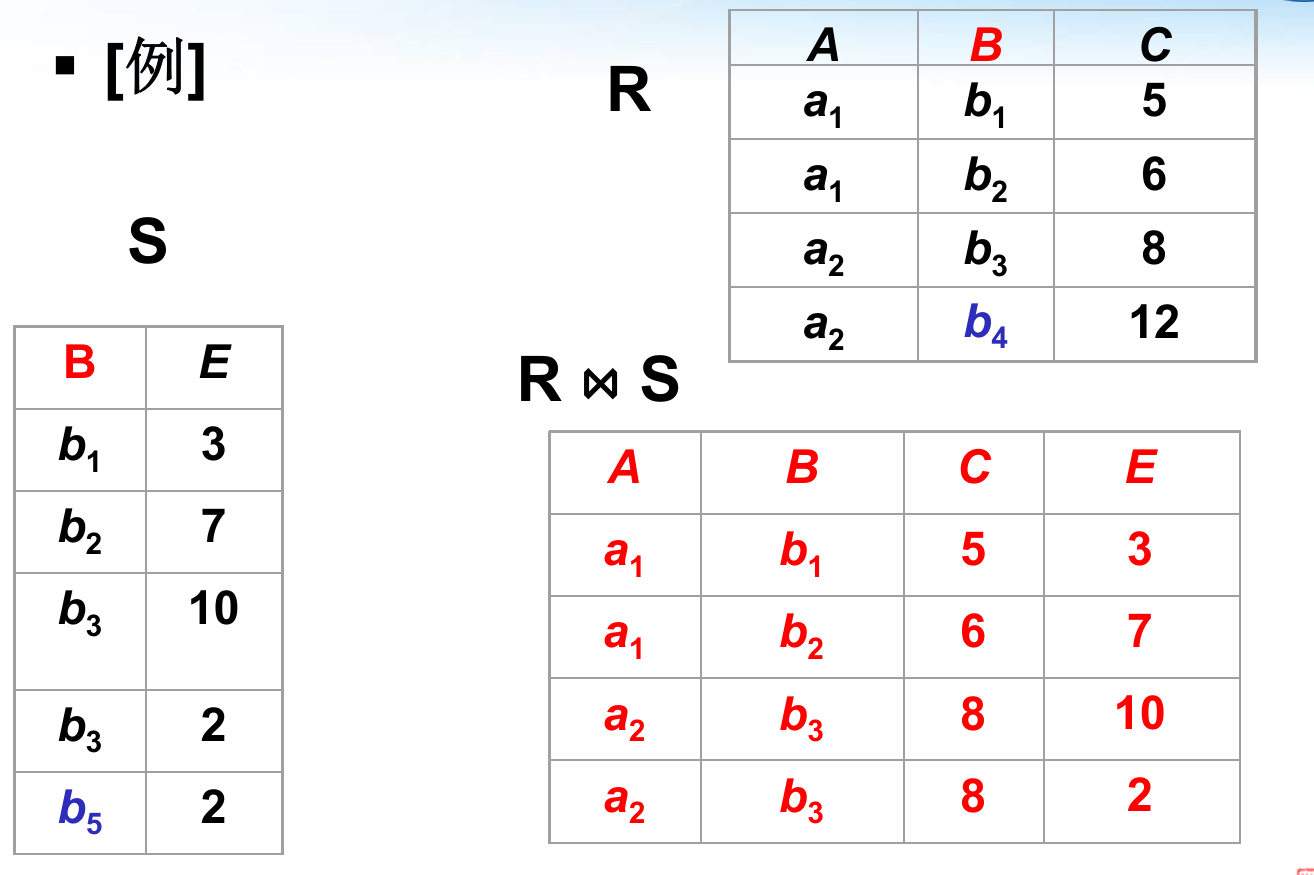
上面介绍的是内连接，还有外连接：

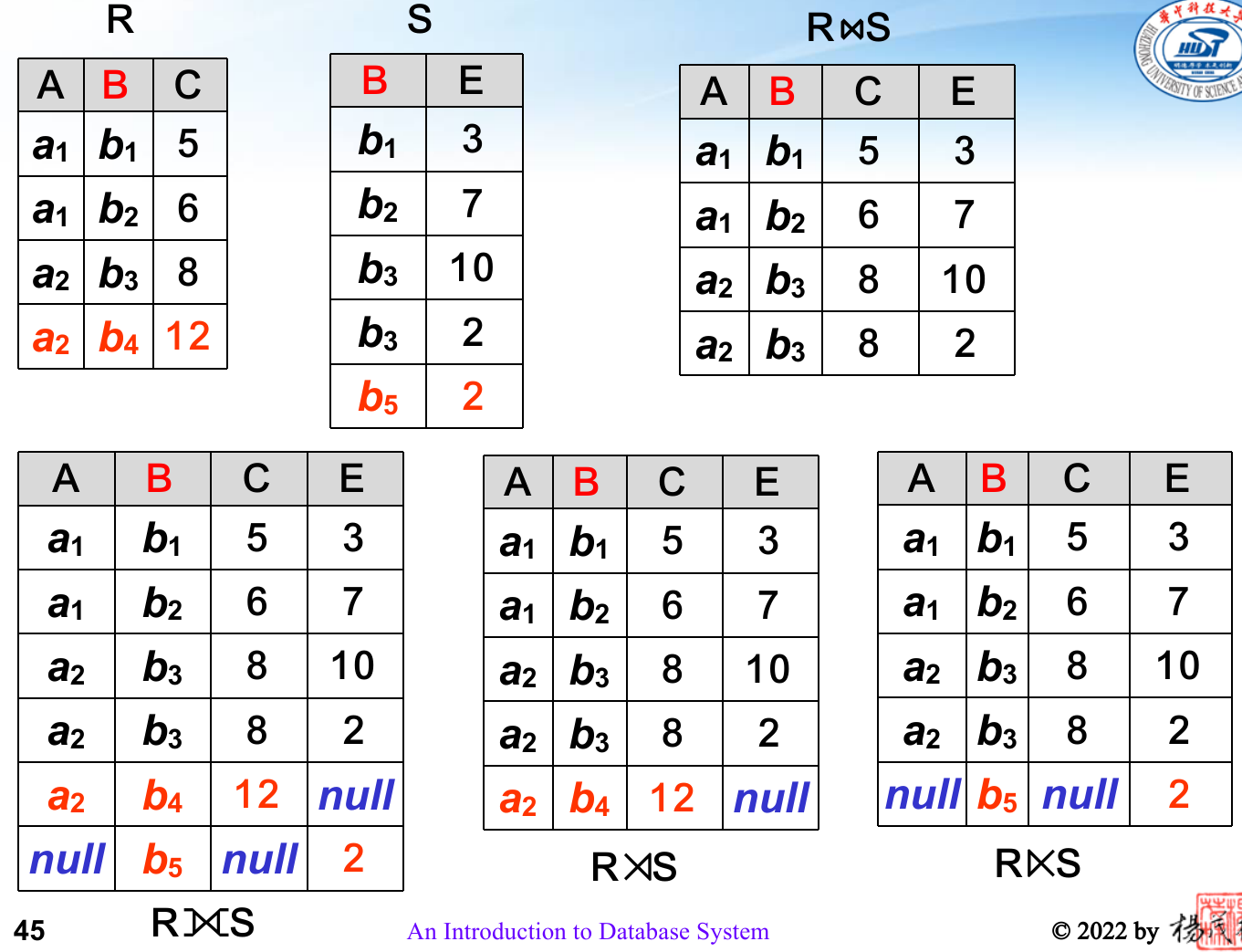
SQL

本章最好看PPT，太复杂了

概述

基本表，可带索引，都放在存储文件里。

视图，只存放定义在数据库中，不存放对应数据，是虚表，概念同基本表。

游标，内存中生成的临时表，相当于指针指向当前处理元组。

数据定义

创建create、删除drop、修改alter

组合上

模式/架构schema、表index、视图view、索引index

数据库database、存储过程procedure、触发器trigger、函数function

在mysql中scheme和database完全等价，SQL server中一个DB可以有多个架构，一个用户可以拥有多个架构，一个架构可以被多个用户拥有，不同架构下允许同名数据对象(db.schema.object)，每个DB有一个缺省的schema叫dbo

schema

create schema 架构名 authorization 用户名

DROP SCHEMA 架构名 <CASCADE | RESTRICT>

CASCADE是级联删除，先删表再删模式。RESTRICT:若架构非空，则拒绝删除

table

create  table   表名（
          列名  数据类型  [<列约束>]
          [，列名  数据类型  [<列约束>]]
          ……
		    [，<表约束>]
）

主码约束： primary key
唯一性约束：unique
非空值约束：not null
参照完整性约束：foreign key
check约束：check(逻辑表达式)

表约束：

表约束可改成列约束(不用指定列名); 约束名可省略

CREATE TABLE SC(
    sno char(9) NOT NULL,
    cno char(4) NOT NULL,
    grade smallint,
    constraint PK_SC primary key(sno, cno),
    constraint FK_SC_SNO foreign key(sno)
          references student(sno),
    constraint FK_SC_CNO foreign key(cno)
          references course(cno)
)
CREATE TABLE SC(
    sno char(9) references student(sno),
    cno char(4) references course(cno),
    grade smallint,
    primary key(sno, cno)
)

索引

聚簇索引最好满足：

被索引的列被经常用于检索
很少对基表进行增删操作
很少对其中的变长列进行修改操作

1
2
3

drop  index  索引名 ON  <object>
drop  index  <object> .索引名
<object> ::= {  数据库名. [架构名] . | 架构名. ]表名}

数据查询

select别名与Where条件

别名可以as、省略as、等号。如果用重名，就用反点号。

select left(sno,4) as  年级,
          sname 姓名,
          院系 = lower(sdept)
from student

where sname like '%\%%' escape '\' 这个escape子句指示转义字符，其他%表示通配

IN ('Ireland', 'Iceland', 'Denmark');检查在不在列表里

BETWEEN 200000 AND 250000闭区间检查

LIKE表模糊查询，%通配许多个字符，_通配一个字符。

concat('%', name, '%')拼接多个字符串

where area >= 3000000 OR population >= 250000000多个条件

ROUND(num, 位数)保留几位小数。位数为1就是保留1位小树，为-3就是对1000取整。

字符串取整用LENGTH()

left(字段, 字符数)取最左边多少个字符。

<>表示不等于

order by可以有多个排序字段order by yr desc, winner，里头甚至可以有逻辑表达式：ORDER BY subject IN ('Physics','Chemistry'), subject,winner表示物理化学的放最后，总体按照学科、获奖者排序。

null 用 is

distinct表示不重复的

一些聚集函数

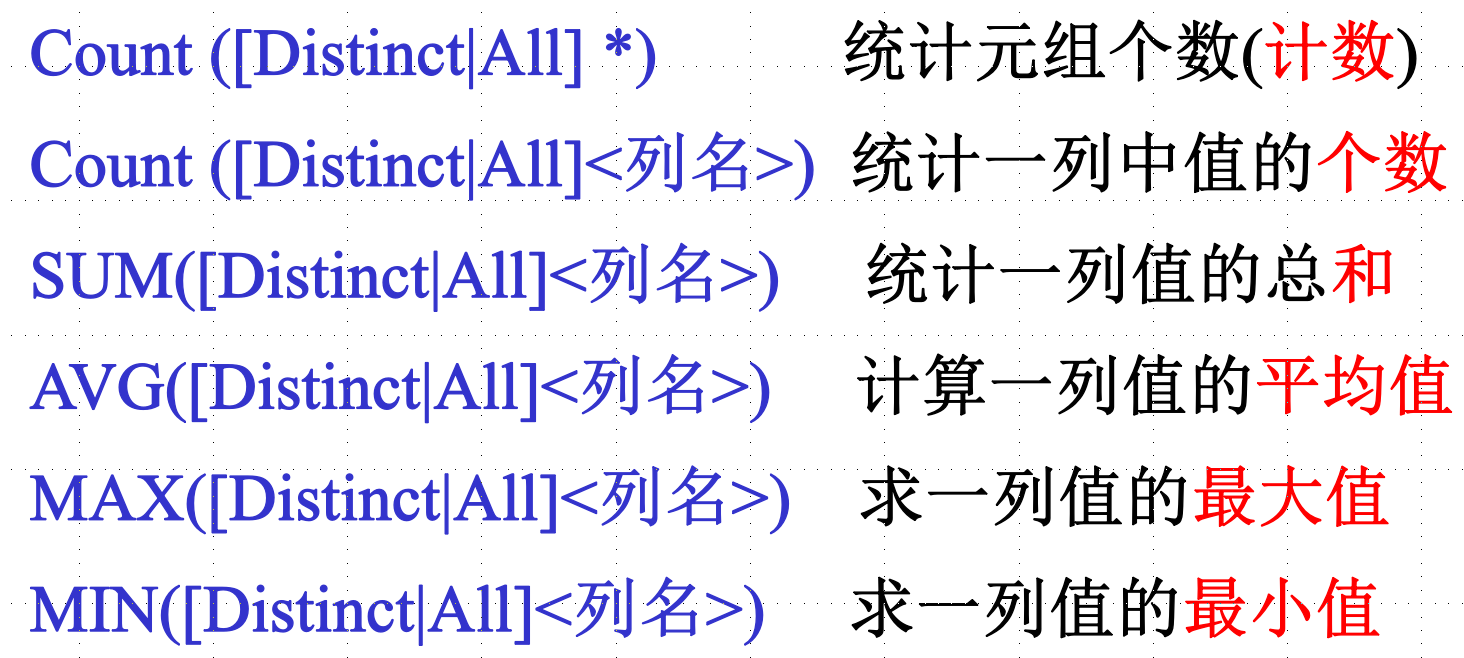
可以用 case when 当三目运算：

1
2
3

CASE WHEN SCORE = 'A' THEN '优'
     WHEN SCORE = 'B' THEN '良'
     WHEN SCORE = 'C' THEN '中' ELSE '不及格' END

COALESCE(x,y,z,...)会返回第一个非空的元素

分组、排序等

“Group By”从字面意义上理解就是根据“By”指定的规则对数据进行分组，所谓的分组就是将一个“数据集”划分成若干个“小区域”，然后针对若干个“小区域”进行数据处理

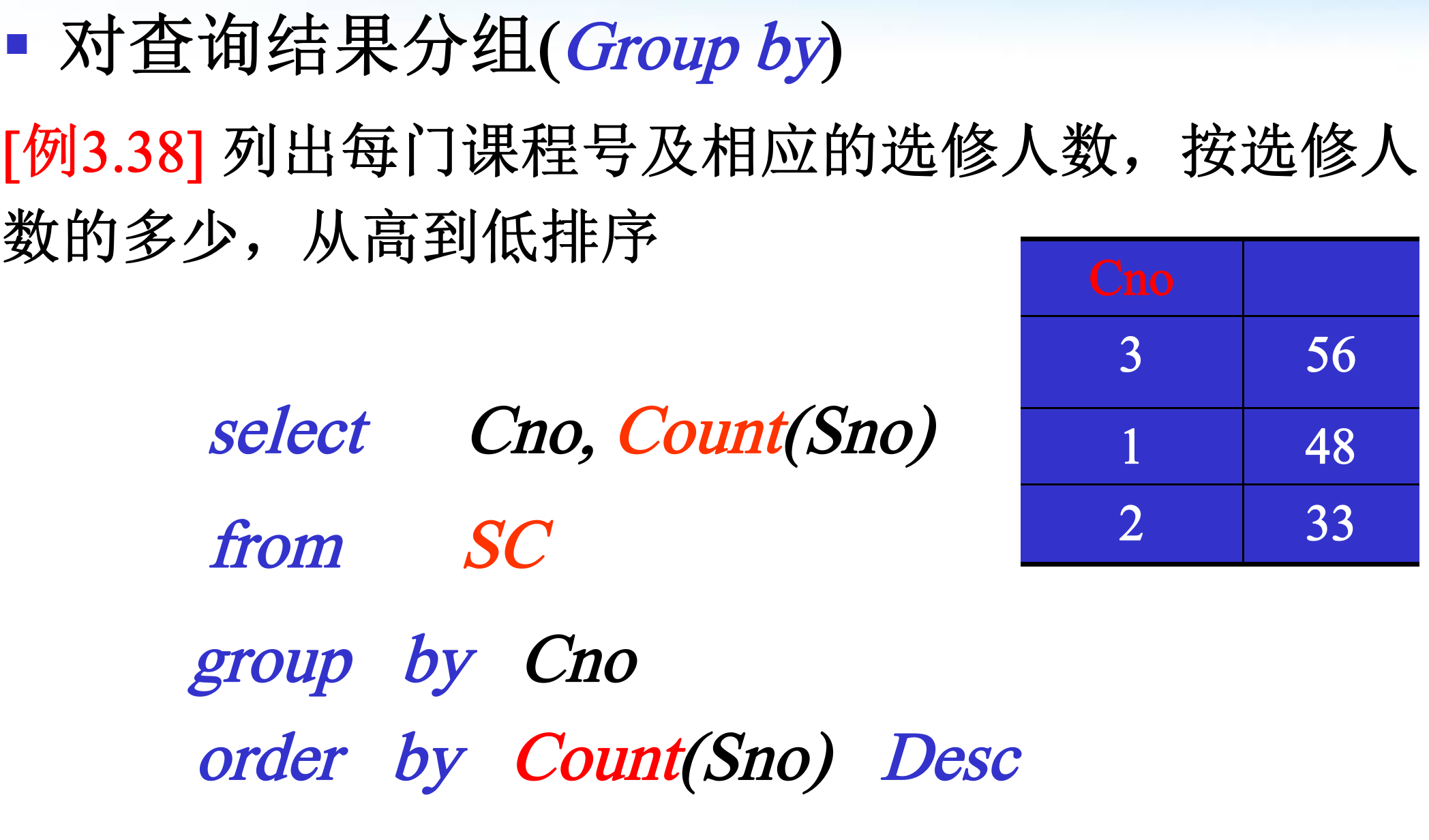
WHERE子句作用于基表或视图，从中选择满足条件的元组。
HAVING短语作用于组，从中选择满足条件的组，它总是跟集函数相关。

group by之后的列表，必包含select列表中除去集函数之后的列表.

Show the years in which three prizes were given for Physics.

nobel(yr, subject, winner)

select yr from nobel
group by yr having sum(subject = 'Physics') = 3;

SELECT yr FROM nobel WHERE subject='Physics'
GROUP BY yr HAVING COUNT(yr)=3;

group by 也可以由多个字段组成。

连接

join在where前面！

列出成绩表上所有学生的学号，姓名，所修课程名称和该课程成绩：

select student.sno,sname,cname,grade
from student, course, sc
where student.sno = sc.sno and
          course.cno = sc.cno

select student.sno,sname,cname,grade
from sc
join student on student.sno = sc.sno
join course on  course.cno = sc.cno

# join 一个
select c_name, c_id_card, total_income
from client join (select pro_c_id, sum(pro_income) total_income from property where pro_status = '可用' group by pro_c_id) as t on client.c_id = t.pro_c_id
order by total_income desc limit 3;

left join：join“右边”的东西可以为空。right full同理。

嵌套查询

嵌套查询如果要大于等于一个子查询的列表，可以使用all，where xxx >= all (select ...)，注意空。

有any、all

内外两个查询都有一样的表名的话记得起别名。

可以用在select from where having里面

子查询里面不能使用order by，前面可以用in、比较、exists

SQL没有全称量词

数据更新

也可以那啥：

数据库安全

数据库安全性控制

授权Grant与回收Revoke

一句只搞一个表

With grant option有了可以转授该权限，没有则不能。不能够循环授权。

With admin option有了可以转授角色。

create user U1 identified by '123456';
create user U2 identified by '123456';
create role R1;
grant all privileges on 学生 to U1 with grant option;
grant all on 班级 to U1 with grant option;
grant all  on * to U1 with grant option;
grant select,update(家庭住址) on 学生 to U2;
grant select,update on 学生 to R1;
grant R1 to U1 with admin option;

revoke 要用from。

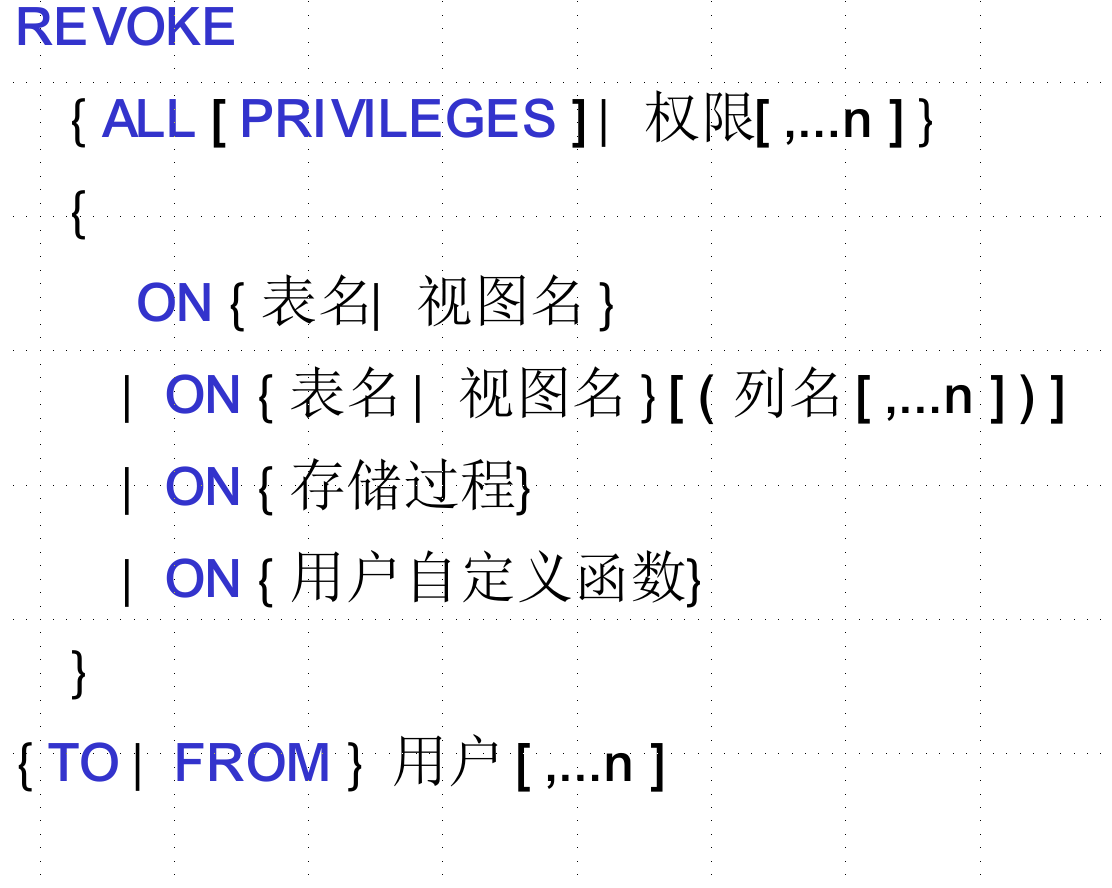
数据库角色

mysql中无login的概念！

GRANT语句可以将权限或角色（权限集合）授予用户或角色。但是不能将权限和角色混合授予用户(或角色)。

也就是说授予权限给角色，授予角色给用户。

强制存取控制方法

数据库完整性

实体完整性

关系模型的实体完整性：CREATE TABLE中用PRIMARY KEY定义

单属性构成的码可以定义为列级约束条件或者表级约束条件

多属性构成的码只能定义为表级约束条件。
alter table xx add/drop ...

在insert、update时检查。主码值唯一否、主码属性为空否。

参照完整性

constraint xx foreign key (col1) references tbl_name(tbl_col)

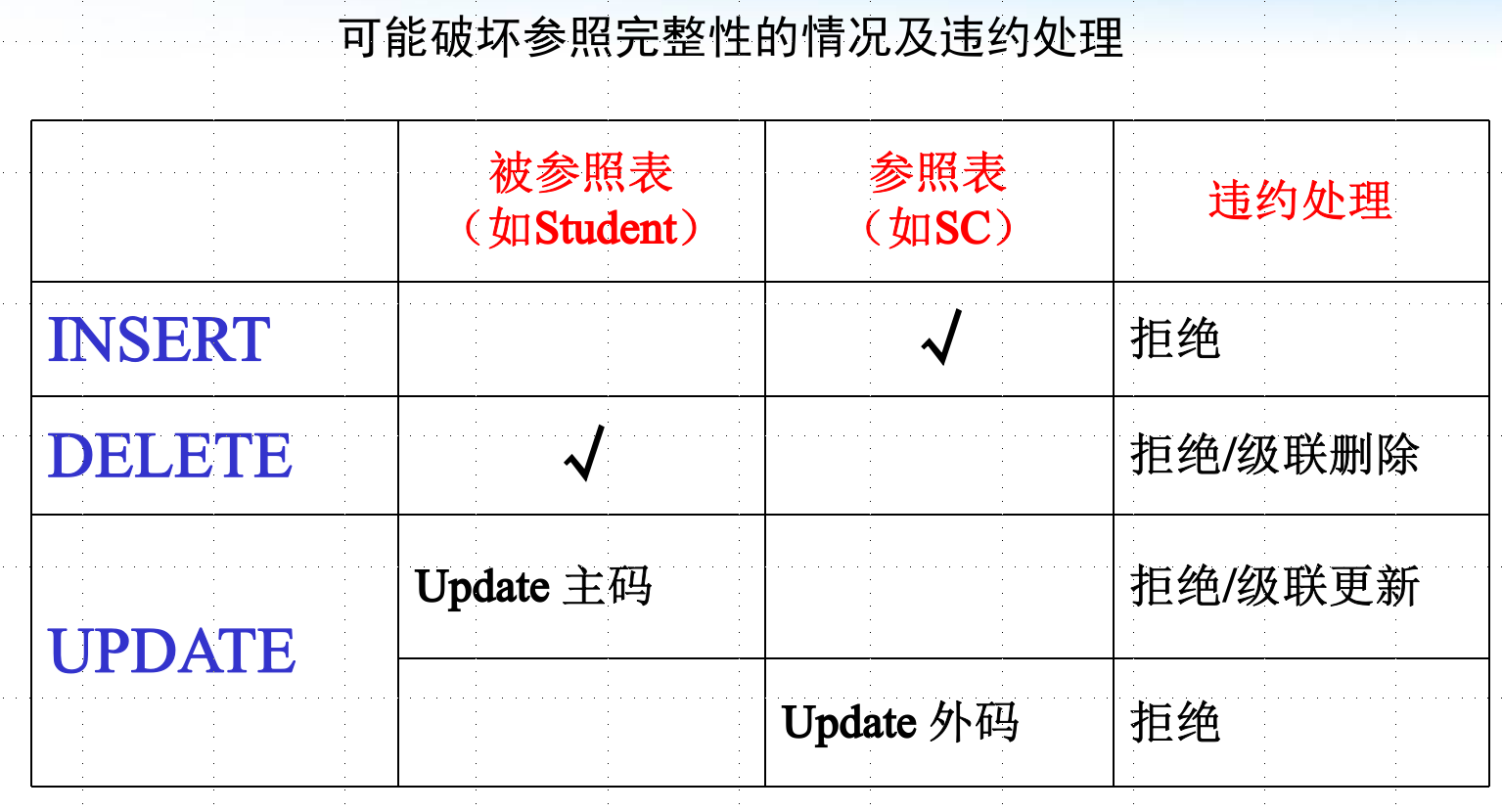
解决：外码列允许为空。级联CASCADE操作。

alter table sc  add
   		constraint FK_S_SC
      		foreign key(sno) references s(sno)
      		on delete cascade on update cascade,
   		constraint FK_C_SC
      		foreign key(cno) references c(cno)
      		on delete cascade on update cascade

用户定义的完整性

NOT NULL和UNIQUE只出现在列约束上
DEFAULT和CHECK约束既可以出现在列约束上，也可以出现在表约束上

域和断言

Domain(域): 带约束的数据类型

Assertion(断言)更复杂、性能更低，他不是一个数据类型

Create domain GENDER char(2)  check(value in (‘男’,’女’))
应用DOMAIN约束列：
Create table s(sno char(4),
                         sname char(10),
                         ssex GENDER)

Create assertion  断言名  check(逻辑表达式)
例：限制最多60名同学选修“数据库”课程：
Create assertion asse_sc_DB_num
Check (60 >= (select count(*) from course,sc
                        where sc.cno = course.cno and
                                   cname=‘数据库’
                        ))

触发器

约束只能访问本行数据，不能跨行、跨表、跨库；约束也无法比较修改前后的数据

这种情况可以用触发器。

1  变量的说明与赋值
DECLARE { @变量名 数据类型 } [ ,...n]
SET|SELECT @局部变量名 = 表达式

2  BEGIN … END语句
BEGIN
    { SQL语句 | 语句块 }
END

3 IF...ELSE语句
IF 布尔表达式
    { SQL语句 | 语句块 }
[ ELSE
    { SQL语句 | 语句块 } ]

4 WHILE语句
WHILE 布尔表达式  { SQL语句 | 语句块 }

5 CASE表达式
CASE  测试表达式
    WHEN  简单表达式  THEN  结果表达式
    [ ...n ]
    [ELSE 结果表达式]
END

5 CASE表达式(续)
CASE
    WHEN 布尔表达式 THEN  结果表达式
    [ ...n ]
    [ ELSE 结果表达式]
END

事务（(A)原子性(C)一致性(I)隔离性(D)持久性）：

Begin transaction
    语句块
commit | rollback

AFTER触发器。在执行完INSERT、UPDATE或DELETE等操作并处理完约束之后执行AFTER触发器。AFTER 触发器只能在表上指定。

instead of 触发器：它指定执行触发器的内容而不是执行引发触发器执行的SQL语句。一个表只能定义一个INSTEAD OF触发器。INSTEAD OF触发器可以定义在视图上。

CREATE TRIGGER trigger_name
{BEFORE|AFTER} {INSERT|UPDATE|DELETE} ON tbl_name FOR EACH ROW

trigger_body

if的写法：if xxx then xxx elseif xxx then xxx else xxx end if;

Inserted(NEW)：新插入的数据(insert时)、更新后的数据(update时)
Deleted(OLD)：被删的数据(delete时)、更新前的数据(update时)
可查询，但不能修改两表的内容

CREATE TRIGGER TRI_INS_GRADE BEFORE INSERT ON SC
FOR EACH ROW
BEGIN
  DECLARE msg varchar(128);
  IF NEW.grade > 100 or NEW.grade < 0
  THEN
     SET msg = concat('Trigger Constraint TRI_INS_GRADE violated: ', cast(NEW.grade as char));
     SIGNAL SQLSTATE '45000' SET MESSAGE_TEXT = msg;
  END IF;
END;

关系数据理论

函数依赖

R(U)：$X , Y \subseteq U$， r是R的任意一个关系，对$\forall s , t \in r$，若s[X] = t[X]，则s[Y] = t[Y]，

则称“X函数确定Y”或“Y函数依赖于X”，记作X→Y。

X称为这个函数依赖的决定属性集(Determinant)。y = f(x)

简单说就是什么决定了什么的问题。

若X→Y，并且Y→X, 则记为X↔Y。

若Y不函数依赖于X, 则记为$X\not \rightarrow Y$ 。

函数依赖是语义范畴的概念，不是根据数据的概念。

X与Y有1:1联系，X→Y，Y→X，即X ↔ Y
X与Y有m:1的联系时，只存在函数依赖X→Y
X与Y有m: n的联系时，则X与Y之间不存在任何函数依赖关系

R(U)：$X , Y \subset U$，若X→Y，且Y⊈ X，则称X→Y是非平凡的函数依赖；若X→Y，但Y $\subseteq$ X, 则称X→Y是平凡的函数依赖。

平凡：就是没劲，自己当然决定自己（而且平凡的函数依赖总是成立的）我们总是讨论非平凡的函数依赖。

R(U)：$X , Y \subset U$，$\forall X’\subset X$，$X\not \rightarrow Y$，则称Y完全函数依赖于X，记作$X\stackrel{f}{\rightarrow}Y$。就是说X决定Y，X不能再小了。

如果存在这么一个X’也能决定Y，就称Y部分函数依赖于X，记作$X\stackrel{p}{\rightarrow}Y$.

在关系模式R(U)中，如果X→Y，Y→Z，且Y⊈ X， Z⊈ Y , Y→X，则称Z传递函数依赖于X。

码和主码：设K为关系模式R<U,F>（F是函数依赖集合）中的属性或属性组合。若$K\stackrel{f}{\rightarrow}U$，则K称为R的一个侯选码（Candidate Key）。若关系模式R有多个候选码，则选定其中的一个做为主码（Primary key）。外码不说了。

函数依赖的公理系统

基本理论

逻辑蕴含：设R <U，F>; 其任何一个关系r，若函数依赖X→Y都成立, 则称F逻辑蕴含X →Y，记作记作$F \vdash X\rightarrow Y$。总之，所有完全、部分、传递函数依赖都搞上了。

函数依赖集的闭包：关系模式R<U,F>中为F所逻辑蕴含的函数依赖的全体所构成的集合称作F的闭包，$F^+ = {X\rightarrow Y | F\vdash X\rightarrow Y}$.

属性集的闭包：设F为属性集U上的一组函数依赖，$X \subseteq U$，$X_F^+ = {A | X\rightarrow A ∈ F^+}$称为属性集X关于函数依赖集F的闭包。F确定的情形下，也可以简写成$X^+$。其实就是通过X能确定的属性的集合。

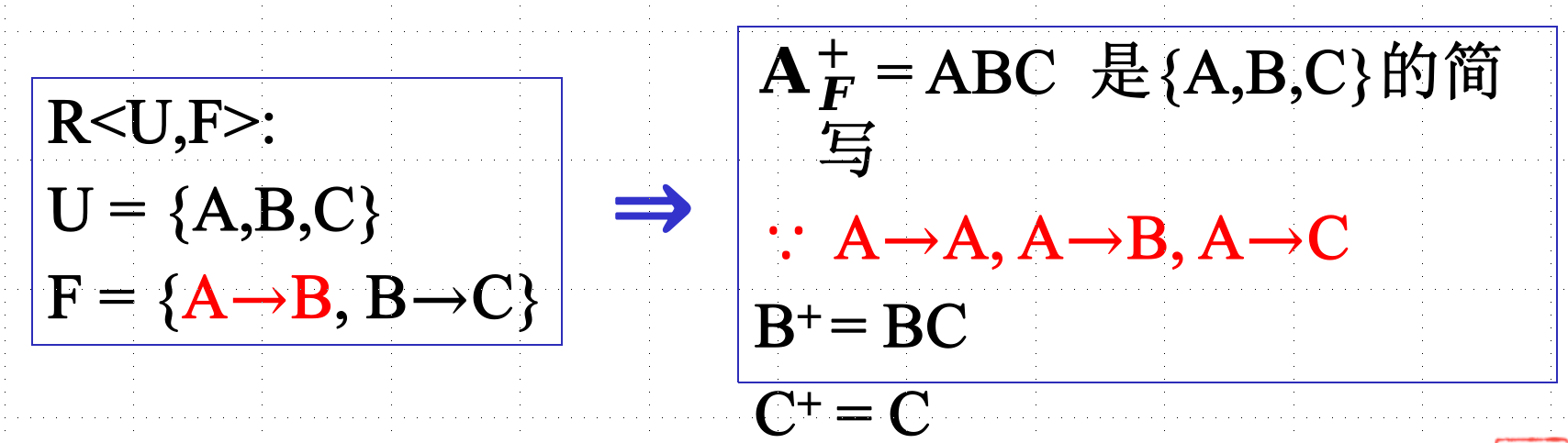
（其中F逻辑蕴含A→B, AB→A, A→C,…反正好多没意思的函数依赖）

Armstrong公理系统：

自反律 $Y\subseteq X ⇒ X→Y$
增广律 $X→Y ⇒ XZ→YZ$
传递律 $X→Y, Y→Z ⇒ X→Z$

可以推导出来：

合并律 $X \rightarrow Y，X \rightarrow Z \Rightarrow X \rightarrow YZ$
分解律 $X\rightarrow Y, Z\subseteq Y \Rightarrow X\rightarrow Z$；特别地，$X\rightarrow YZ \Rightarrow X \rightarrow Y，X \rightarrow Z$
伪传递律 $X \rightarrow Y，WY \rightarrow Z\Rightarrow WX \rightarrow Z$

以及几个重要引理：

$X\rightarrow A_1 A_2 \cdots A_k \Leftrightarrow X\rightarrow A_i (i=1, 2, \ldots ,k) $
$X→Y \Leftrightarrow X_F^+ ⊇ Y$
$V→W，X_F^+ ⊇ V ⇒ X_F^+ ⊇ W$

计算属性集的闭包，可以来回扫描函数依赖，直到闭包集不变化：

如果$G^+=F^+$，就说函数依赖集F覆盖G（F是G的覆盖，或G是F的覆盖），或F与G等价。

$ F^+ = G^+ \Leftrightarrow F \subseteq G^+，G \subseteq F^+$

求极小函数依赖集

每一个函数依赖集F均等价于一个极小函数依赖集$F_m$。（它不是唯一的）

三步循环走：单属性化、无冗余化、既约化；单属性化、无冗余化、既约化；单属性化、无冗余化、既约化……

单属性化：利用分解律，将所有函数依赖右部单属性化

无冗余化：逐一检查F中各函数依赖X→Y，令G=F-{X→Y}，若$X_G^+⊇ Y$ ，则从F中去掉此函数依赖。

既约化：去掉依赖左部的多余属性：

正则覆盖

正则覆盖不要求右侧单属性，恰恰相反，它要求左侧相同的依赖要合并成一个
正则覆盖不单单寻找左侧多余的属性，它寻找两侧多余的属性

如果去掉一个函数依赖中的属性不改变该函数依赖集的闭包，则称该属性是无关属性。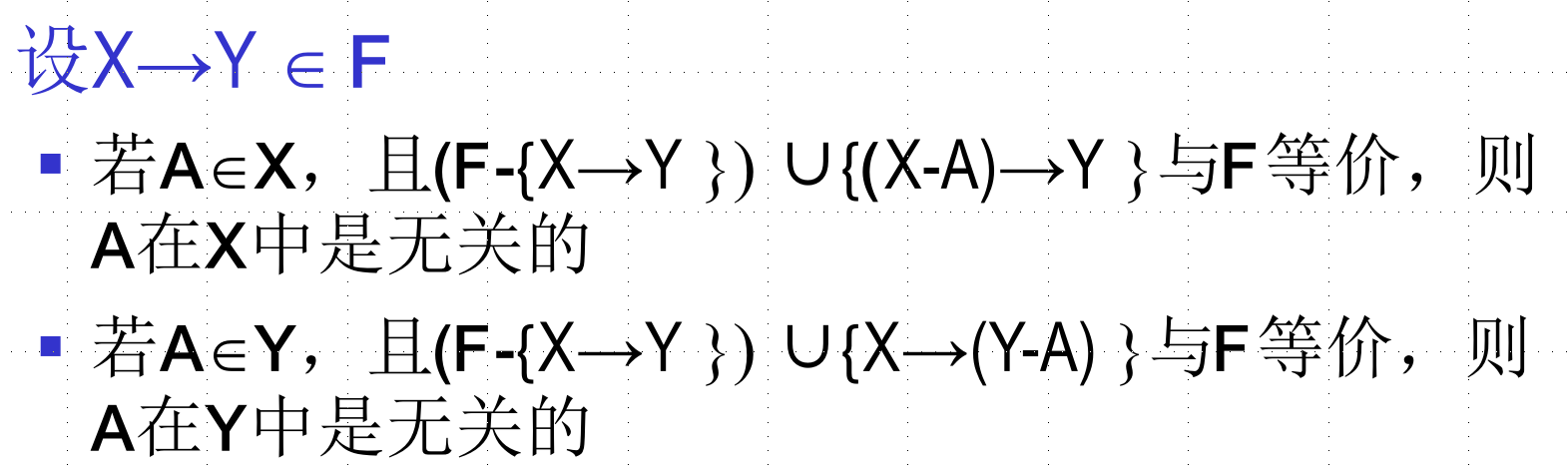

两步循环走：

使用合并律合并左侧相同的函数依赖
找出每个函数中的无关属性，并去之

求关系模式R<U,F>候选码

仅在函数依赖右部出现的属性集称为纯R属性集，记为RO(Right Only)；
不在任何函数依赖右部出现的属性集为独立属性集，记为N；
在函数依赖左右部均出现的属性集称为双边属性集，记为LR；

不在任何函数依赖右部出现的属性必出现在每个候选码中(一定是主属性)

仅在函数依赖右部出现的属性一定不是主属性
(不会出现在任何候选码中)

范式与规范化

1NF

任给关系模式R(U,F)，若U中每个属性及其值均为不可再分的基本数据元素（原子项），则R∈1NF。

消除非主属性对码的部分依赖，规范化(投影分解)：

所有完全FD于码的属性组成一个关系模式
所有部分FD于码的属性组成另一个关系模式

解决了1NF的这些问题，就是2NF了：

2NF

若关系模式R∈1NF，并且每一个非主属性都完全函数依赖于R的码，则R∈2NF。

(不存在非主属性对码的部分函数依赖)
推论: 若R∈1NF,且其候选码为单个属性,则R∈2NF

要投影分解,消去非主属性对码的传递依赖。

解决了2NF的这些问题，就是3NF了：

3NF

关系模式R<U，F> 中若不存在码X、属性组Y及非主属性Z（Z ⊈ Y）, 使得X→Y，$Y \not → X$，Y→Z，成立，则称R<U，F> ∈ 3NF。

(属性不依赖于其它非主属性 [ 消除传递依赖 ],要求一个数据库表中不包含已在其它表中已包含的非主关键字信息。)

关系模式R的所有非平凡函数依赖，要么左侧包含候选码，要么右侧是主属性。（定义2）

例如，员工信息表Staff中已经包含部门编号dept_id，那么就不能再包含dept_name, dept_location等信息。

BCNF

R<U，F>∈1NF，若X→Y，且Y ⊈ X 时X必含码，则R∈BCNF。

所有非平凡函数依赖左侧必包含候选码。

R∈BCNF，则R∈3NF

例如，StorehouseManage(仓库ID, 存储物品ID, 管理员ID, 数量)，(仓库ID, 存储物品ID) →(管理员ID, 数量)，(管理员ID, 存储物品ID) → (仓库ID, 数量)

但是存在如下决定关系：(仓库ID) → (管理员ID)，(管理员ID) → (仓库ID)，即存在关键字段决定关键字段的情况，所以其不符合BCNF范式

因此分解成仓库管理：StorehouseManage(仓库ID, 管理员ID)；仓库：Storehouse(仓库ID, 存储物品ID, 数量)。

多值依赖

放弃了

描述型定义：设R(U)是一个属性集U上的一个关系模式， X、 Y和Z是U的子集，并且Z＝U－X－Y，多值依赖 X→→Y成立当且仅当对R的任一关系r，给定一对(x, z）的值，有一组Y的值与这对应，这组值仅仅决定于x值而与z值无关。

若X→→Y，而Z＝φ，则称X→→Y为平凡的多值依赖
否则称X→→Y为非平凡的多值依赖

4NF

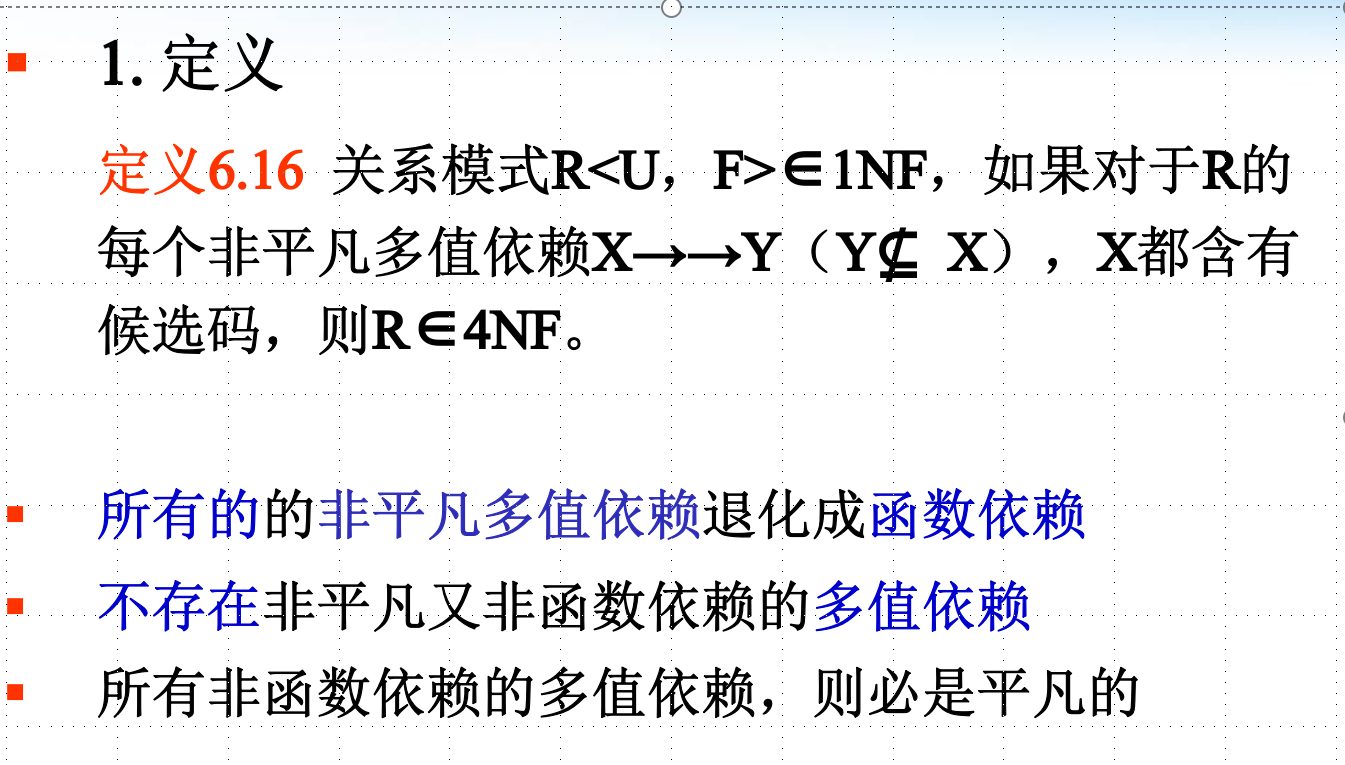
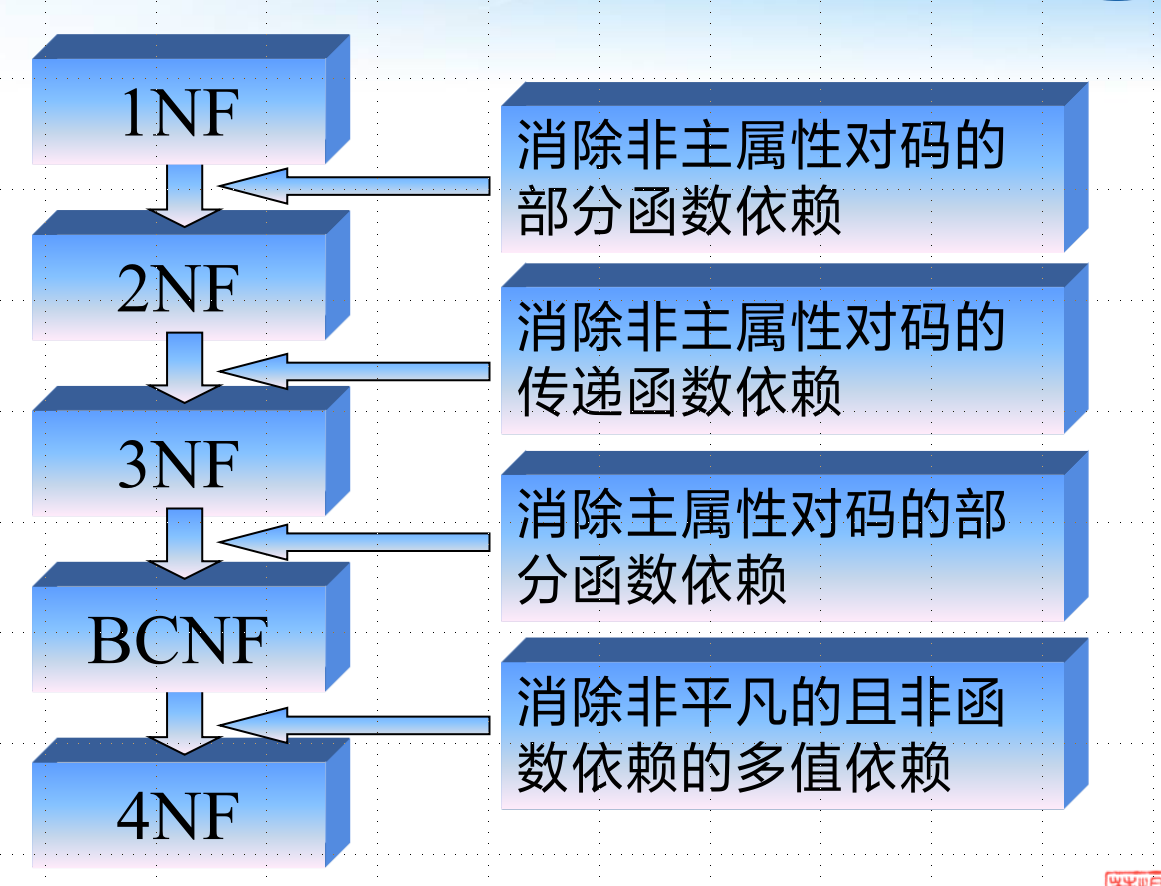
BCNF说是在3NF的基础上消除了一切属性对码的部分、传递函数依赖比较好。

关系模式的分解

无损连接分解

就是分解以后再join！

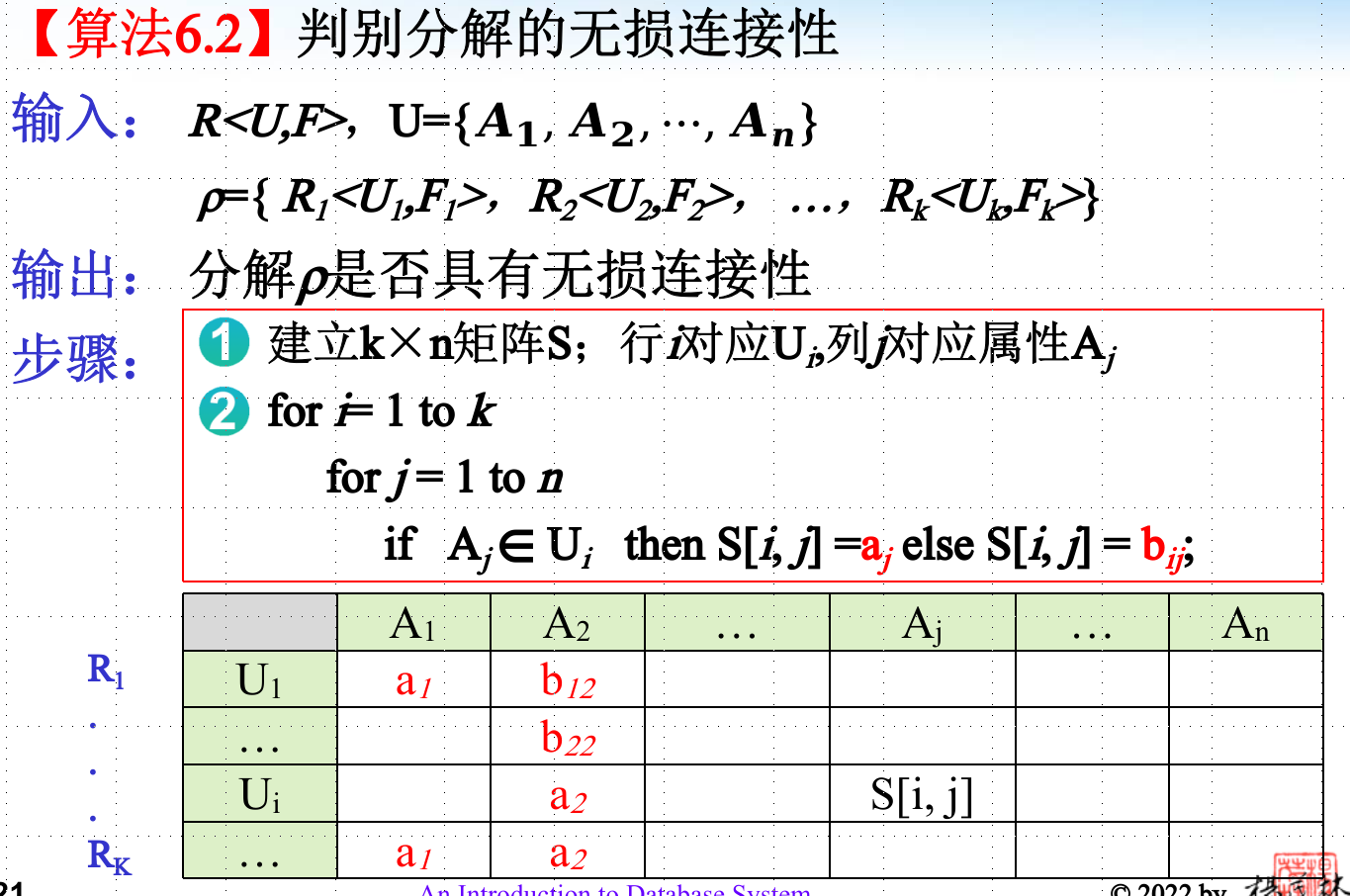
保持函数依赖的分解

数据库设计

建立索引的考虑：

如果一个(或一组)属性经常在查询条件中出现，则考虑在这个(或这组)属性上建立索引(或组合索引)
如果一个属性经常作为最大值和最小值等聚集函数的参数，则考虑在这个属性上建立索引
如果一个(或一组)属性经常在连接操作的连接条件中出现，则考虑在这个(或这组)属性上建立索引

为了提高某个属性（或属性组）的查询速度，把这个或这些属性（称为聚簇码）上具有相同值的元组集中存放在连续的物理块称为聚簇

聚簇索引的索引项顺序与表中元组的物理顺序一致。
在一个基本表上最多只能建立一个聚簇索引。

当一个关系满足下列两个条件时，可以选择HASH存取方法：

该关系的属性主要出现在等值连接条件中或主要出现在相等比较选择条件中
该关系的大小可预知，而且不变 / 该关系的大小动态改变，但所选用的DBMS提供了动态HASH存取方法。

关系数据库引擎基础-SP

我感觉这一节不太会考。

数据库存储

从效率、安全等角度出发，主流DBMS都倾向于自己进行页面管理。

文件组织：基于链表的堆文件O(n)，基于页目录的堆文件类似哈希表。而堆文件是一个无序的page集合，其中的元组可按随机顺序存放，支持page的创建、读、写和删除操作，支持遍历所有pages的操作

基于链表的堆文件，堆文件头部设立一个header page，并存放两个指针，分别指向：空页列表（free list）头部、数据页列表（data list）头部。每个page均记录当前空闲的空间（slot）

（感觉就是俩双向链表）

基于目录的堆文件：

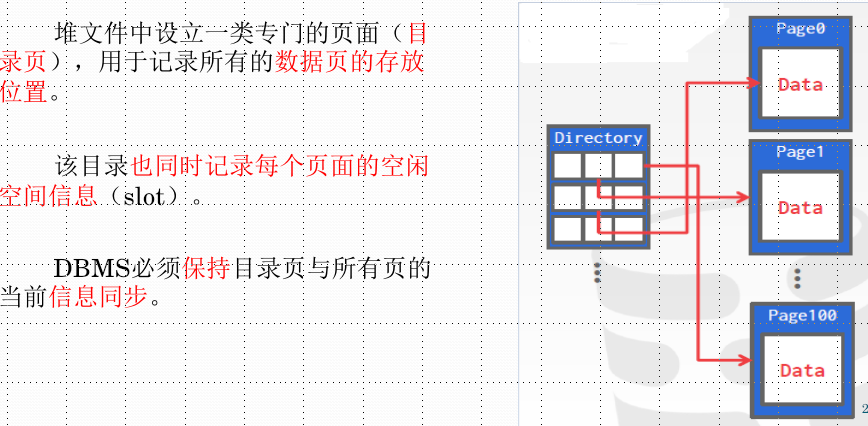
一个页只存放一类信息（元组、元数据、索引、日志记录）

每个页具备一个唯一ID，单文件可以是offset，多文件一般会有个间接层映射页面id到文件的路径和offset

硬件页面是存储设备中能保证故障安全写操作（failsafe write）的最大数据块单位。每个页有页头。

页面内“数据”的组织方式：

面向元组型
日志结构型

面向元组型的页设计就是嗯append元组，对删除元组和变长元组支持不好，更长见的是：

槽页（Slotted Pages）

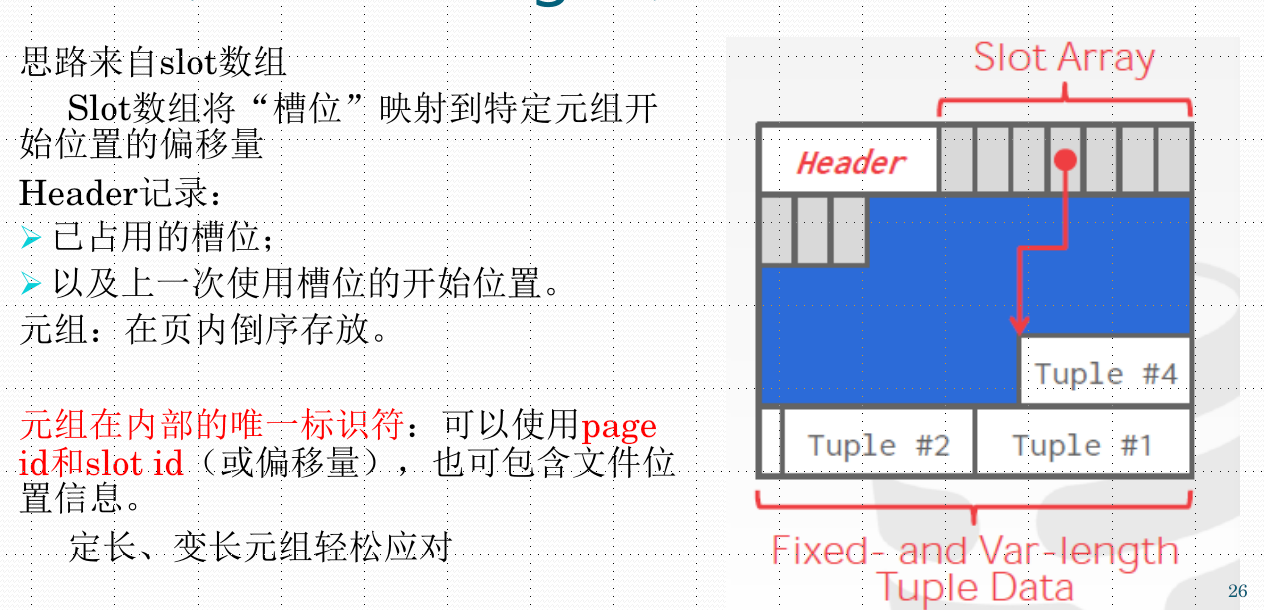
日志式文件记录，页中只存放日志记录

联机事务处理（On-Line Transaction Processing，OLTP），传统具较强“事务特性”需求的应用，比如电商、贸易等
联机分析处理（On-Line Analytical Processing，OLAP），数据量较大，主要是查询、复杂查询、统计，甚至数据挖掘

复合事务分析处理（Hybrid Transaction-Analytical Processing，HTAP）兼具OLTP和OLAP特征

常见的n元存储模型（n-ary storage mode，NSM，又名“行存储”）非常适合OLTP。此时，单个元组的所有属性连续的分布在一个page中，查询往往涉及单个实体（工作量较少），并能适应较为繁重的“更新”工作量

针对OLAP，分解存储模型（Decomposition Storage Model，DSM）更为适合，又称为“列存储”，DBMS将单个属性的值连续的组织在一个page中；
可以很好的适应大数据量、复杂查询语义、高负载查询。

缓存

当执行引擎操作那部分内存时，缓冲池管理器必须确保该页面始终驻留在那片内存区域中。

缓冲池管理器的目标：尽可能减少磁盘I/O带来的延时。

用于缓存页面的内存空间被组织为一个数组，其中每个数组项被称为一个帧，一个帧正好能放置一个页面。

页表是缓冲池管理器用于维护缓冲池元数据的数据结构。维护位置信息、脏标志、引用计数。

锁lock是事务级别的，保护的是表、元组这种逻辑对象，持续时间长，可以回滚

闩latch是线程级别的，保护的是内部数据结构，一般用os机制实现，不考虑回滚。

散列表

散列函数特性：

函数的输出是确定的
输出值的分布是随机且均匀的
易于计算

线性探测法：

如果散列值对应的桶中已有数据，则将数据存放到相邻的桶中。
查找时，从散列值对应的位置开始向后搜索。直至找到key值或者空桶。

但是删除时，要注意避免影响将来的查找。可以用墓碑法或者移位法。

链式散列表：

每个桶指针指向一个链表，散列值相同的数据拉链存放。

可扩展散列表：以二倍翻倍

线性散列表：以奇怪的关系扩展

查询处理

迭代模型（火山模型）：不断执行Next函数，得到元组或者一个null标记。

物化模型：

物化模型适合OLTP.

向量模型：和迭代模型差不多，不过返回的是一批元组而不是一个

至于数据存取方法，有三种：

顺序扫描

索引扫描（多索引一般用求交集的方法）

关系查询处理和查询优化-SP

关系数据库系统的查询处理

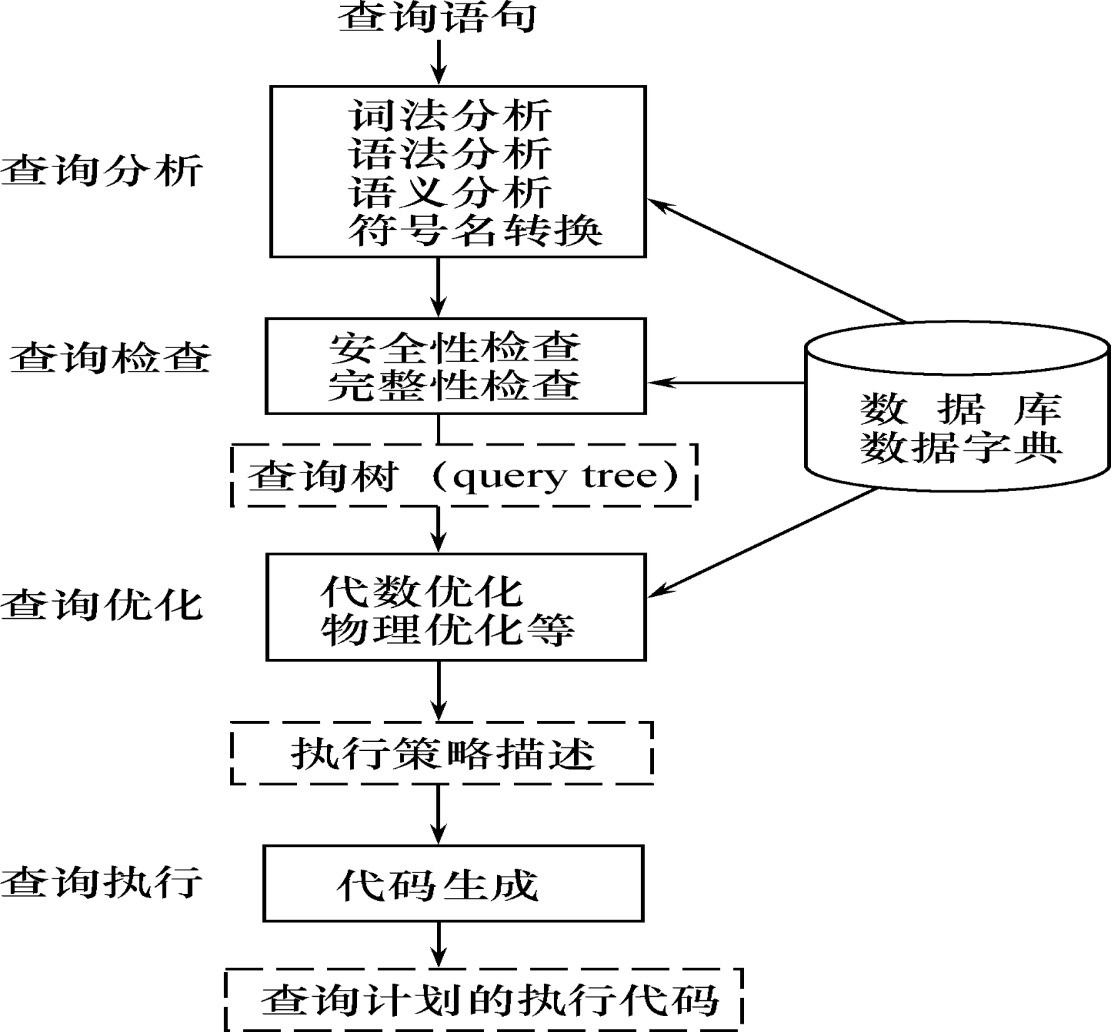
查询分析
查询检查
查询优化
查询执行

选择操作典型实现方法：
（1）全表扫描方法
（2）索引扫描方法

连接操作的实现：

嵌套循环方法(nested loop)
排序-合并方法(sort-merge join 或merge join)
索引连接(index join)方法
哈希连接(Hash Join)方法

关系数据库系统的查询优化

也许会出分析题吧。分析块数量。

代数优化

关系代数表达式的优化

代数优化的查询树启发式优化规则：

选择运算应尽可能先做！！！（减小中间集的规模）
投影和选择运算同时进行（避免重复扫描）
将投影运算与其前后的双目运算结合起来（避免重复扫描）
某些选择运算＋其前面的笛卡尔积 ⇒ 连接运算（减小中间集的规模）
提取公共子表达式(公因子)（保存计算结果，避免重复计算）

总的来说，算法就是四步：

分解选择运算
通过交换选择运算，将其尽可能移到叶端
通过交换投影运算，将其尽可能移到叶端
合并选择和投影的串接

物理优化

嵌套循环怎么计算块数？

这个只是读的，写的时候要继续考虑

数据库恢复技术-SP

基本概念

事务是恢复和并发控制的基本单位

事务的ACID特性：

原子性（Atomicity）
一致性（Consistency）
隔离性（Isolation）
持续性（Durability ）

恢复的目标：ACD没有I

事务故障：某个事务在运行过程中由于种种原因未运行至正常终止点就夭折了，比如溢出，死锁牺牲，业务要求

系统故障：使系统停止运转的事件；OS得重启

介质故障：硬件故障使存储在外存中的数据部分丢失或全部丢失

事务故障时，夭折的事务可能已把对数据库的部分修改写回磁盘

系统故障时，只有外部存储设备上的数据未受影响

事务故障的恢复

反向扫描日志文件（即从最后向前扫描日志文件），查找该事务的更新操作。
对该事务的更新操作执行逆操作。即将日志记录中“更新前的值”（Befor Image, BI）写入数据库。
1. 插入操作， “更新前的值”为空，则相当于做删除操作
2. 删除操作，“更新后的值”为空，则相当于做插入操作
3. 修改操作，则用BI 代替 AI（After Image）
继续反向扫描，对下一个更新操作作同样处理。
直到读到此事务的开始标记。

系统故障的恢复

正向扫描日志文件（即从头扫描日志文件）
1. Redo队列: 在故障发生前已经提交的事务
2. Undo队列:故障发生时尚未完成的事务
对Undo队列事务进行UNDO处理
反向扫描日志文件，对每个UNDO事务的更新操作执行逆操作
对Redo队列事务进行REDO处理
正向扫描日志文件，对每个REDO事务重新执行登记的操作

介质故障的恢复

略

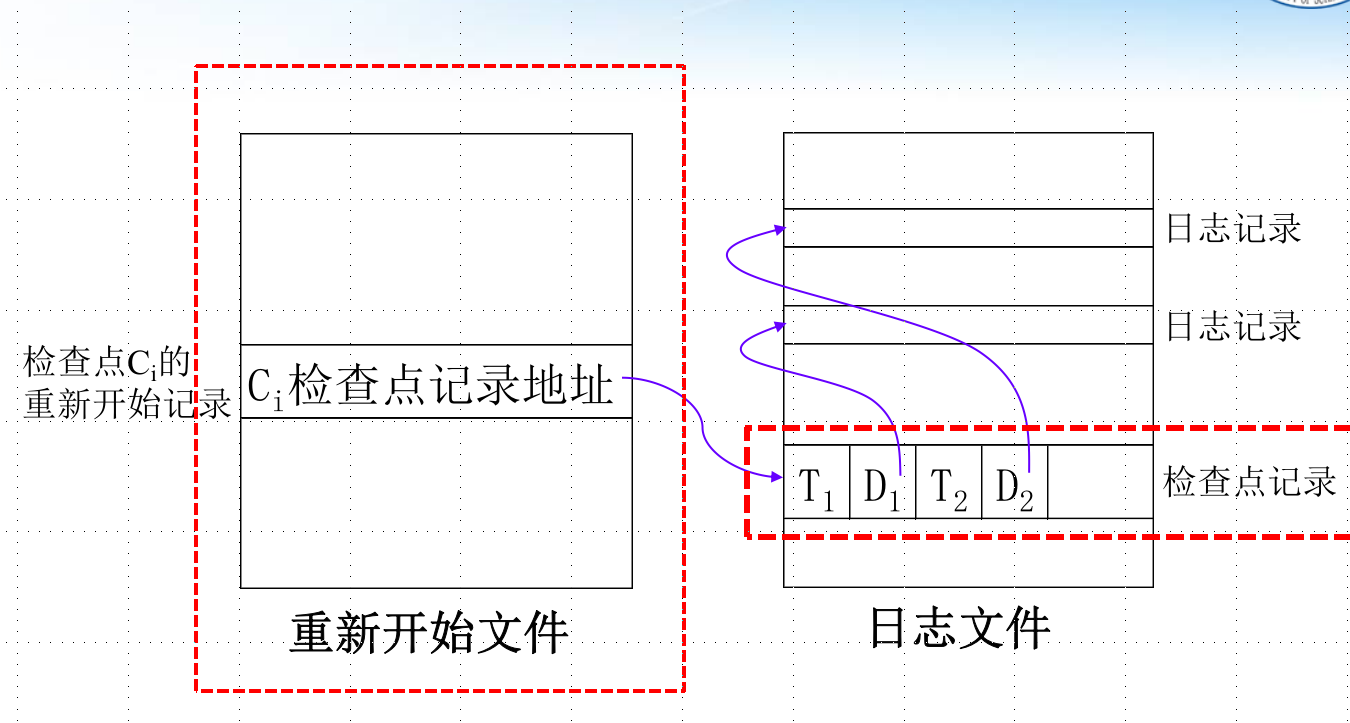
具有检查点的恢复技术

在日志文件中增加检查点记录
增加重新开始文件
恢复子系统在登录日志文件期间动态地维护日志

检查点记录的内容：建立检查点时刻所有正在执行的事务清单，这些事务最近一个日志记录的地址

重新开始文件的内容：记录各个检查点记录在日志文件中的地址

并发控制

更新于 2024-05-28

# 笔记 # 数据库

数据库笔记

复习要点

绪论

关系模型

SQL

数据库安全性

完整性

关系数据理论

数据库的设计 15%

代数优化

恢复

并发控制

第八章 存储引擎

绪论

文件系统与数据库系统的区别

层次模型，网状模型，关系模型

关系模型

三级模式，二级映像，数据独立性

数据模型，数据库系统的结构和组成

关系数据库

三类关系，三类完整性

关系数据结构

关系代数

分量和象集

关系运算

SQL

概述

数据定义

schema

table

索引

数据查询

select别名与Where条件

分组、排序等

连接

嵌套查询

数据更新

数据库安全

数据库安全性控制

授权Grant与回收Revoke

数据库角色

强制存取控制方法

数据库完整性

实体完整性

参照完整性

用户定义的完整性

域和断言

触发器

关系数据理论

函数依赖

函数依赖的公理系统

基本理论

求极小函数依赖集

正则覆盖

求关系模式R<U,F>候选码

范式与规范化

1NF

2NF

3NF

BCNF

多值依赖

4NF

关系模式的分解

无损连接分解

保持函数依赖的分解

数据库设计

关系数据库引擎基础-SP

数据库存储

缓存

散列表

查询处理

关系查询处理和查询优化-SP

关系数据库系统的查询处理

关系数据库系统的查询优化

代数优化

物理优化

数据库恢复技术-SP

基本概念

事务故障的恢复

系统故障的恢复

第八章存储引擎