过!过!过!
引论和课程重点
编译过程:词法分析、语法分析、语义分析、中间代码生成、代码优化、目标代码生成
第一章大概10%
第二章文法语言肯定要给语言要求使用文法描述,可以结合第三章
自顶向下分析肯定会考一个完整的
LR也会考一个完整的
算符优先,简单优先可能不会考完整的,只会考一个概念
几种LR的关系要知道
第七八章要考,可能会考翻译模式,给c让你翻译中间代码。
第九章考一个栈帧就行了
具体的开完会再说
课程重点选择来源:作业里有的、PPT后面写的重点
ch02-文法和语言
设计一个已知语言的文法;确定已知文法定义的语言;求句型的短语、直接短语和句柄;文法二义性判定
ch03-词法分析
设计正规文法|正规式|有穷自动机;等价转换;词法分析器的构造
ch04-自顶向下语法分析方法
- 计算产生式的SELECT()集
- FIRST()集,FOLLOW()集
- 判断文法是否LL(1)文法
- LL(1)分析表
- LL(1)分析算法
- 递归子程序构造
- 非LL(1)文法:提取左公因子,消除左递归,改造或重新设计文法,使其成为LL(1)文法
ch05-自底向上优先分析
计算优先关系;优先文法的判定;构造优先分析表;优先分析算法
ch06-LR分析
基本概念:
可归前缀、活前缀、LR(0)项目、移进项目、待约项目、归约项目、接受项目、移进-归约冲突、归约-归约冲突、LR(0)项目集、LR(0)项目集规范族、LR(0)文法、SLR(1)文法、搜索符、搜索集、LR(1)项目、LR(1)文法、LR(1)项目集规范族、同心项目、同心项目集和LALR(1)文法
重点掌握:
- 构造识别LR(0)活前缀DFA、构造识别LR(1)活前缀DFA和合并识别LR(1)活前缀DFA的同心项目集;
- LR(0)、SLR(1)、LR(1)和LALR(1)文法判别;
- LR(0)、SLR(1)、LR(1)和LALR(1) 分析表;
- LR分析算法。
ch07-语法制导的语义分析
属性文法基本概念与属性的计算方法;翻译模式基本概念与属性的计算方法
ch08-静态语义分析和中间代码生成
符号表的作用于基本实现技术;表达式的中间代码表示;基本语法规则的语义规则设计
ch09-运行时存储组织
静态数组、动态数组、关键字池、浮动地址代码、静态数据对象、动态数据对象、静态存储分配、栈式动态存储分配、堆式存储分配、过程活动记录和静态层次数
ch10-代码优化与目标代码生成
基本块划分
程序流图构造
循环的识别
循环的优化
文法和语言
符号和符号串-文法的基本要素
字母表∑是非空有穷集合,其元素称为符号。由字母表∑中的符号组成的有穷序列称为 (字母表∑上的)符号串. 不含任何符号的有穷序列称为空串,记为ε。符号串α的长度是指符号串α中含有符号的个数,记为︱α︱。如果集合A的元素都是字母表∑上的符号串,则称集合A为∑上的符号串集合,简称串集。
设字母表∑={a,b,c},A={ε,a,ba,cab},B={a1,ba,cab},则 A是∑上的符号串集合,B不是∑上的符号串集合。
符号串的运算:和计算理论中的类似。连接、或、幂、正闭包、星闭包。
符号串集合的运算:(笛卡尔)乘积、和、幂、正闭包、星闭包。

显然,若A为任意一个字母表,$A^*$就是字母表上所有符号串(包括空串)的集合。
文法和语言的形式化定义
 $\alpha ::= \beta$简写为$\alpha \rightarrow \beta$。若P中包含它,则任意的串γαδ 可以推导出γβδ,这是直接推导/一步推导,记为γαδ $\Rightarrow$ γβδ。也可以说γβδ归约到γαδ ,这种归约称为直接归约/一步归约。
$\alpha ::= \beta$简写为$\alpha \rightarrow \beta$。若P中包含它,则任意的串γαδ 可以推导出γβδ,这是直接推导/一步推导,记为γαδ $\Rightarrow$ γβδ。也可以说γβδ归约到γαδ ,这种归约称为直接归约/一步归约。

若$\alpha \stackrel{+}{\Rightarrow} \beta$或者$\alpha \rightarrow \beta$,则记$\alpha \stackrel{*}{\Rightarrow} \beta$。
句型和句子:G[S] 有$S \stackrel{}{\Rightarrow} \beta$,则称β是文法G[S]的句型。若β∈$V_T^$,则称β是文法G的句子。当然,句子也是句型。
文法G产生语言即为其句子的集合,记为L(G)。如果两个文法的产生语言一样,文法就等价。
文法的类型
0型文法/短语文法/图灵机:一个文法的所有规则,左侧至少含有一个非终结符。
1型文法/上下文有关文法/线性界限自动机:左侧符号串的长度不大于右侧符号串的长度(空规则除外),且左侧至少含有一个非终结符。( γAδ $\Rightarrow$ γβθδ,A被替换成βθ,跟A的上下文相关,因为要match整个 γAδ)
2型文法/上下文无关文法:任一产生式左部均为恰好一个非终结符
3型文法/正规文法/有限自动机:跟教材上不一样!

L3真含于L2真含于L1真含于L0。
上下文无关文法及其语法树
最右推导,也叫规范推导。由规范推导所得的句型,叫做规范句型(右句型)。规范推导的逆过程,叫做规范归约。
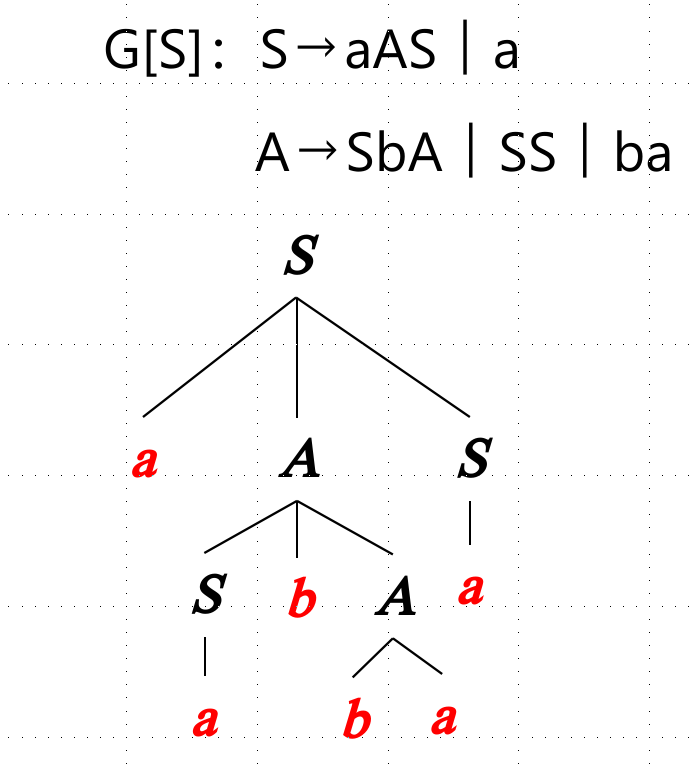
语法的二义性不等于语言的二义性。二义性文法可能存在等价的非二义性文法。不过语法的二义性问题是不可判定的。
句型的分析
假设文法G[S]是语言L之文法,即L(G)=L,则“符号串α是否符合语言L的语法问题” 被等价地转化成“推导或归约问题”,即是否$S \stackrel{}{\Rightarrow} \alpha \and \alpha \in V_T^$。
自顶向下分析法:从文法开始符号出发,反复使用规则,寻找匹配符号串(推导)的句型,直到推导出句子或穷尽规则也不能推导出。
要解决的问题:选择句型中哪一个非终结符进行推导、选择非终结符的哪一个规则进行推导。
容易出现回溯,可以考虑提公因子。
自下而上分析法:从输入符号串α开始,逐步进行“归约”,直至归约出文法的开始符号 S,则输入串α是文法G定义的语言的句子,否则不是
要解决的问题:如何选择句型α的子串β进行归约。
按句柄归约-规范归约(移进-归约)
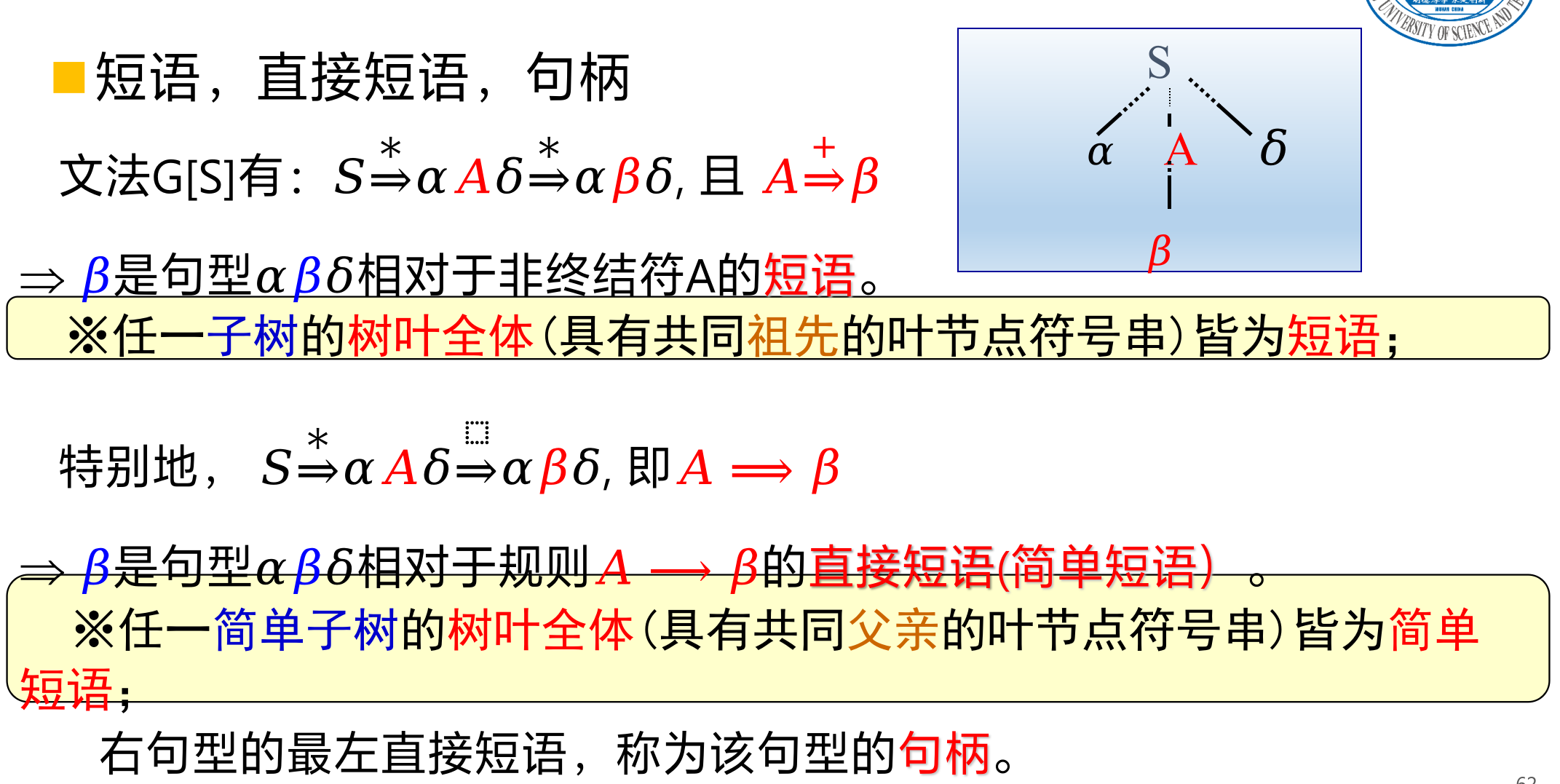
总的来说,一个非终结符的树叶组成短语,一个下面就一层的非终结符的树叶组成直接短语。在做推导的时候,ε直接不写。但是在分析短语的时候,ε要写出来。一个句型最左边的那一个直接短语,叫做句柄

补充说明-文法中的多余规则和epsilon (ε) 规则
文法的化简:
删除A->A这样的有害规则
删除不终结产生式(永远到不了终结符)
删除不可用产生式(压根到不了规则左边的非终结符)
删除ε产生式:

词法分析
词法分析程序设计
输出每个词形式 (单词种别,单词自身的值),单词种别常用enum
单词的形式化描述工具
用正规文法、正规式、有穷自动机三种描述方法。(计算理论人狂喜)
正规文法:设文法G=($V_N$,$V_T$,P,S),如果任意A→β∈ P,A∈ $V_N$ ,且β只能是aB或a或Ɛ, 则称文法G属于右线性3型文法。
正规式:算符优先级由高到低 :*,·,|
有穷自动机
DFA的f: 状态转换(移)函数,为$K\times \Sigma \rightarrow K$的单值部分映射
DFA的扩展状态转移函数 f’ $K\times \Sigma^* \rightarrow K$,编译的DFA好像允许不是每个字母都有状态去转移
NFA的状态转移函数 $K\times(\Sigma\cup{ε})\rightarrow P(K)$,其中P(K)为K的幂集
NFA 弧上的标记可以是ε,同一个字母可能出现在同一状态射出的多条弧上
NFA

每次都做集合到集合的变换

显然$\epsilon-Closure(I)$就是I通过空转移能到达的所有状态的集合
各类转换
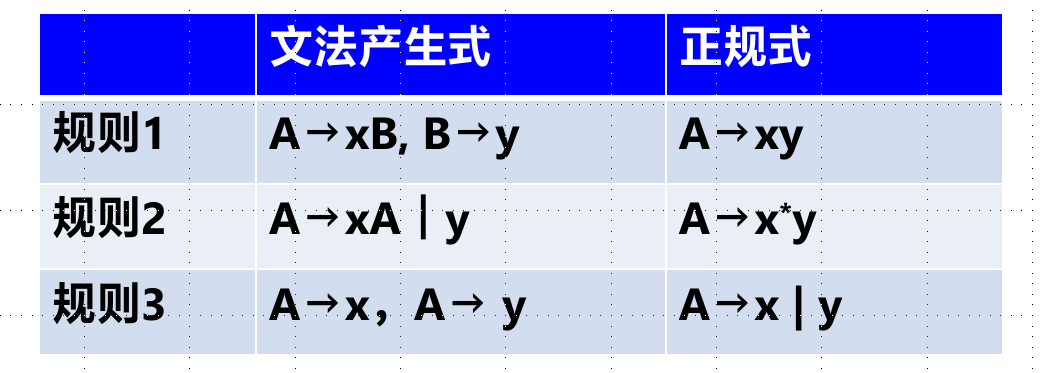
正规式转正规文法

我的评价是计算理论重现江湖
正规文法转正规式
NFA转DFA
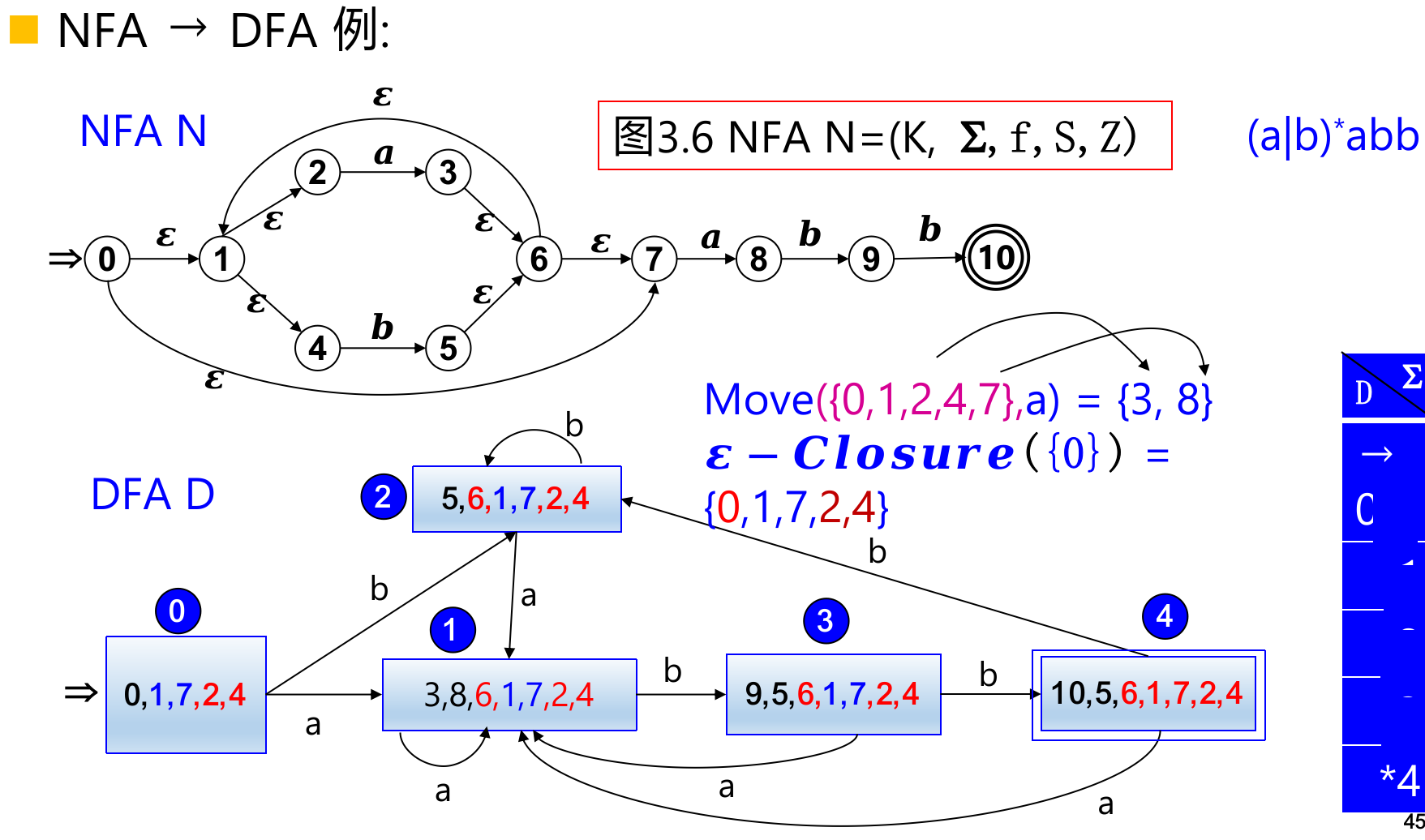
画这么一个表:
| 重命名 | a | b | |
|---|---|---|---|
| {0,1,7,2,4} | 0 | {3,8,6,1,7,2,4} | {5,6,1,7,2,4} |
| {3,8,6,1,7,2,4} | … | … | … |
就是首先放进去ε-Closure(S),然后不断变换。注意每一个变换的结果都是ε-Closure。最后按这个表格重命名画图。
DFA的化简
- 消除无用状态:不可达,没有通路到达终态;
- 合并等价状态(都是终结态/非终结态,任意转换都到等价的状态)
起初的两个集合先按终结 非终结分类,每次查看有没有一个集合的两个元素的转移结果不在同一个集合里头,那么这两个元素就要拆开。

正规式和有穷自动机的转换
NFA转正规式:
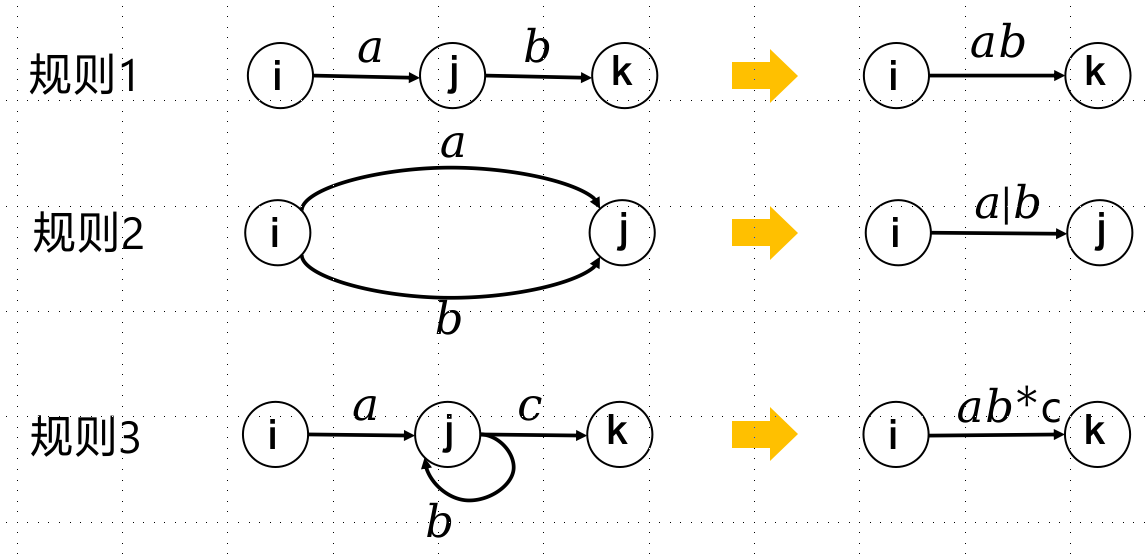
正规式转NFA:
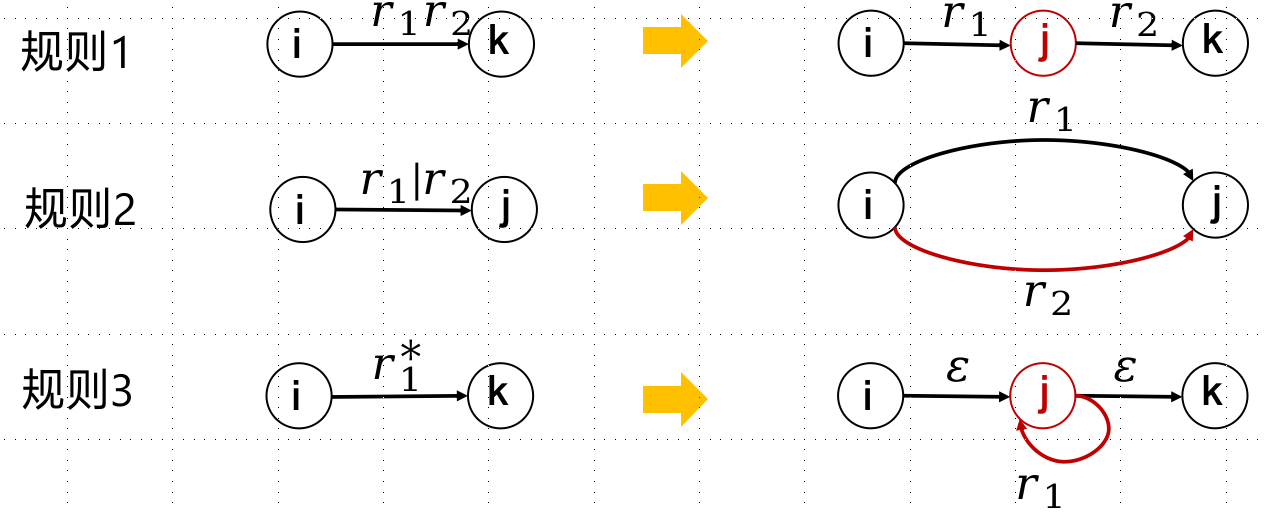
NFA转DFA就是了。
正规文法和有穷自动机的转换

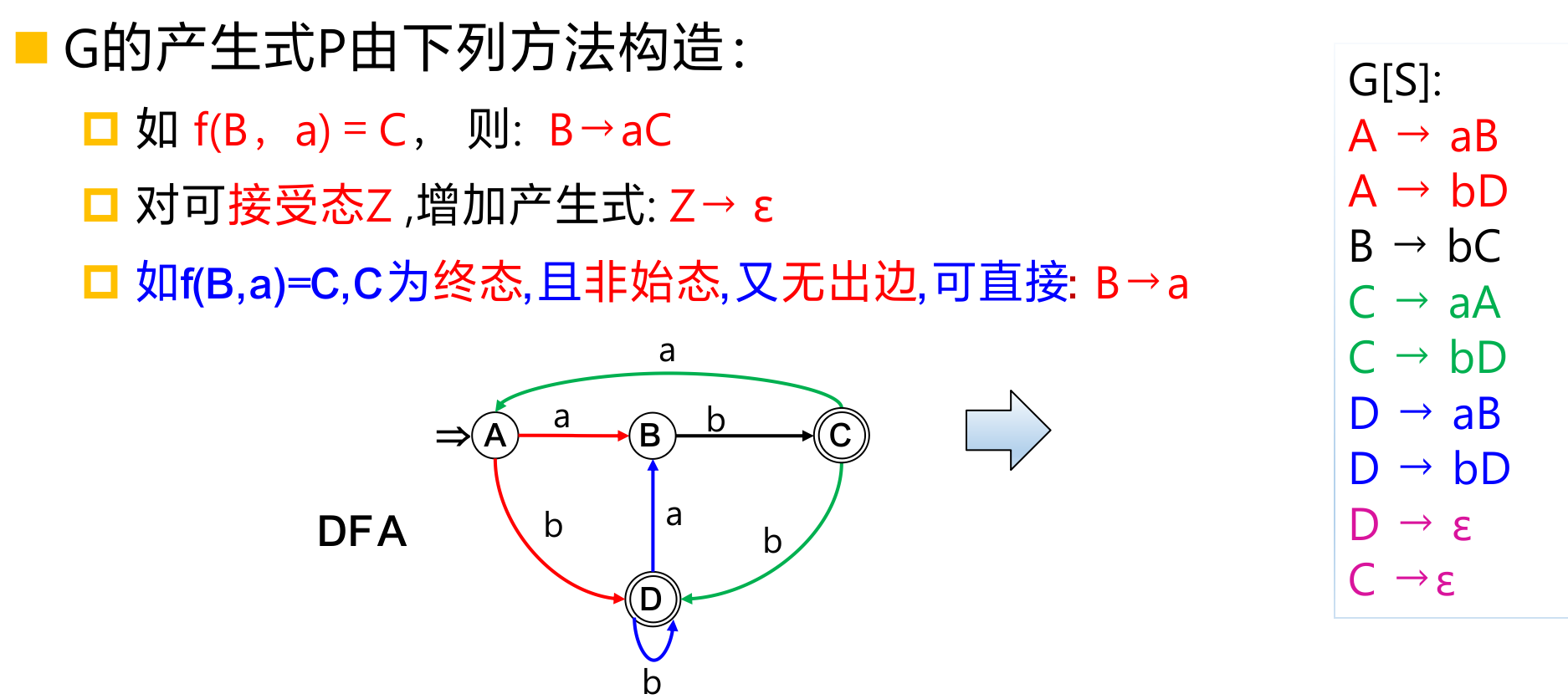
自顶向下语法分析方法
自顶向下是推导,ANTLR4,LL(1)
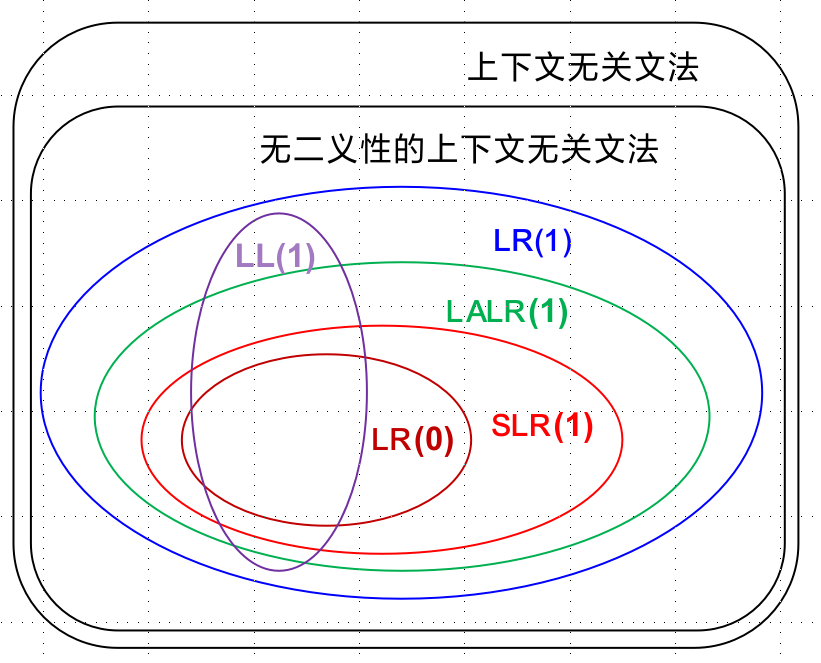
确定的自顶向下语法分析思想
约定好每次选择最左边的非终结符,选择出来一个唯一的产生式
FIRST(α)-串首(终结)符号集

FOLLOW(A)-非终结符的后继(终结)符号集。FOLLOW(A)是由任意句型中紧邻非终结符号A之后出现的终结符号a组成的集合。


SELECT(A→α) - 产生式的可选集

文法G是LL(1)的,当且仅当对每个VN,A的两个不同产生式A→α,A→β,满足SELECT(A→α) ∩ SELECT(A→β) = Φ 其中,α、β不能同时推导出ε。确定的无二义性的。
L – Left to right parsing 从左至右分析token
L – Left-most derivation 最左推导
1 –只需向右看1个符号便可以决定选择哪个产生式进行推导

LL(1)文法的判别
文法G是LL(1)的,当且仅当任意两个左部相同的产生式其select集的交集为空。
- 判别$S \stackrel{*}{\Rightarrow} \alpha$ ?仅当α中所有非终结符全部可推导出空,且α无非空的终结符
- 求产生式右部FIRST集, 如产式右部可推导出ε,则还需:
- 计算产生式左部FOLLOW集
判别能否产生空串:

求产生式右部FIRST集:

求follow集合:

某些非LL(1)文法到LL(1)文法的等价变换
若文法含有左公共因子,或者含有直接或间接左递归,一定不是LL(1)文法。
先消除左递归,再提取左公因子。
提取左公因子:

这么不断提取。注意没有左公因子只是一个必要条件。
消除左递归:


消除一切左递归:

LL(1)分析的实现-递归下降分析法
将每个非终结符编写成一个递归子程序,选择规则的实现步骤是将输入串“下一个符号”逐个与A规则的选择集进行判定。
LL(1)分析的实现-表驱动分析法

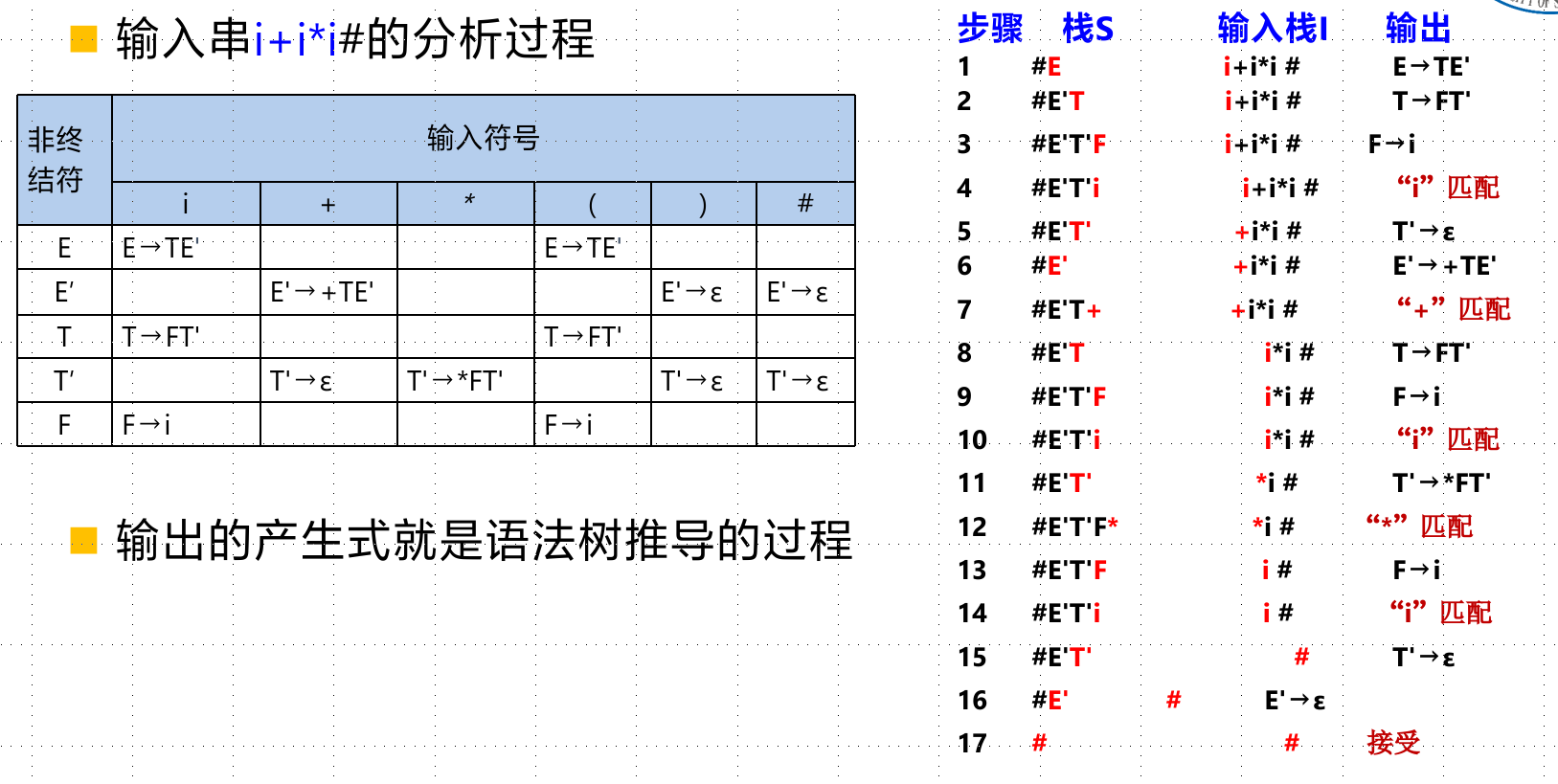
自底向上优先分析
简单优先分析法

文法G的符号集V中,任意两个符号之间至多$\lessdot$lessdot、$\gtrdot$gtrdot、$\eqcirc$eqcirc(实在打不出来了)三种简单优先关系之一,且没有相同右部的规则,则文法G称为简单优先文法。

算符优先分析法


设不含空规则的文法G为OG文法,如果任意两个终结符之间至多存在$\eqcirc,\lessdot,\gtrdot$三种算符优先关系之一,则称文法G为算符优先文法(Operator Precedence Grammar),简称OPG文法。

后面太复杂了,做了作业再截图





实例
注意:任何句型前后都有一个井号!自己加的。
竖着的是a,横着的是b,内容是a和b的关系
N代表任意非终结符,感觉是根据前一个非终结符的关系来判定,小于和等于就移进。大于规约。
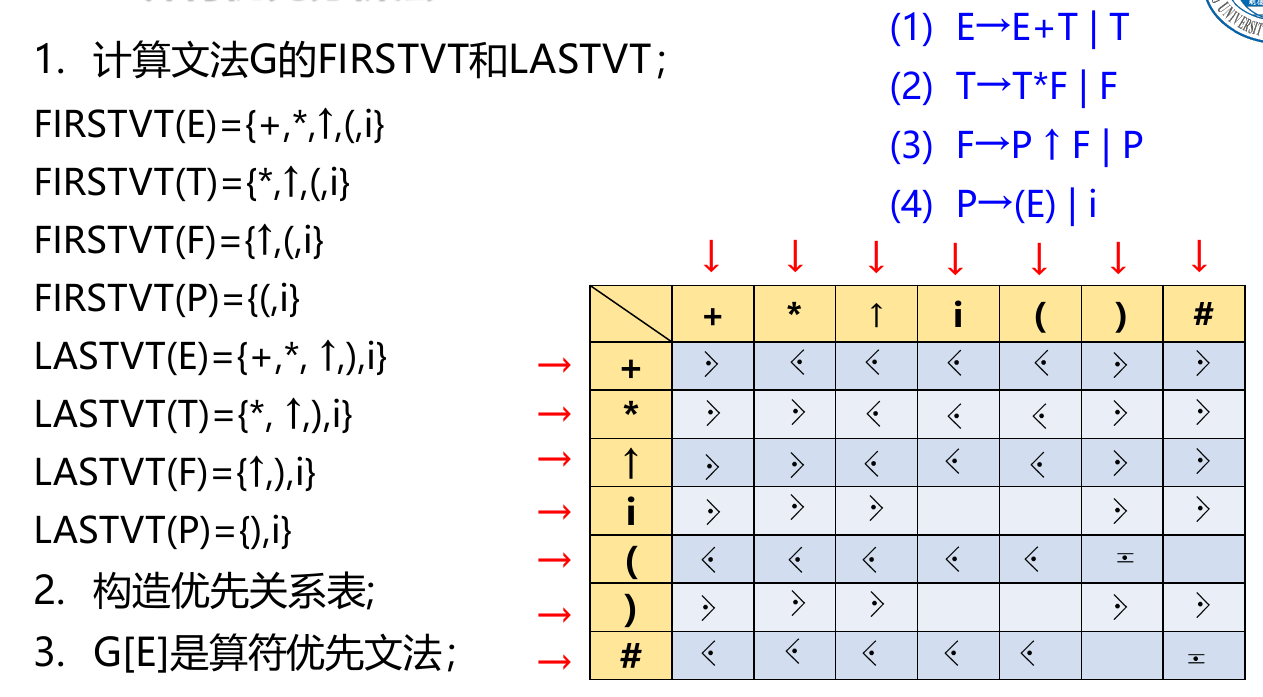
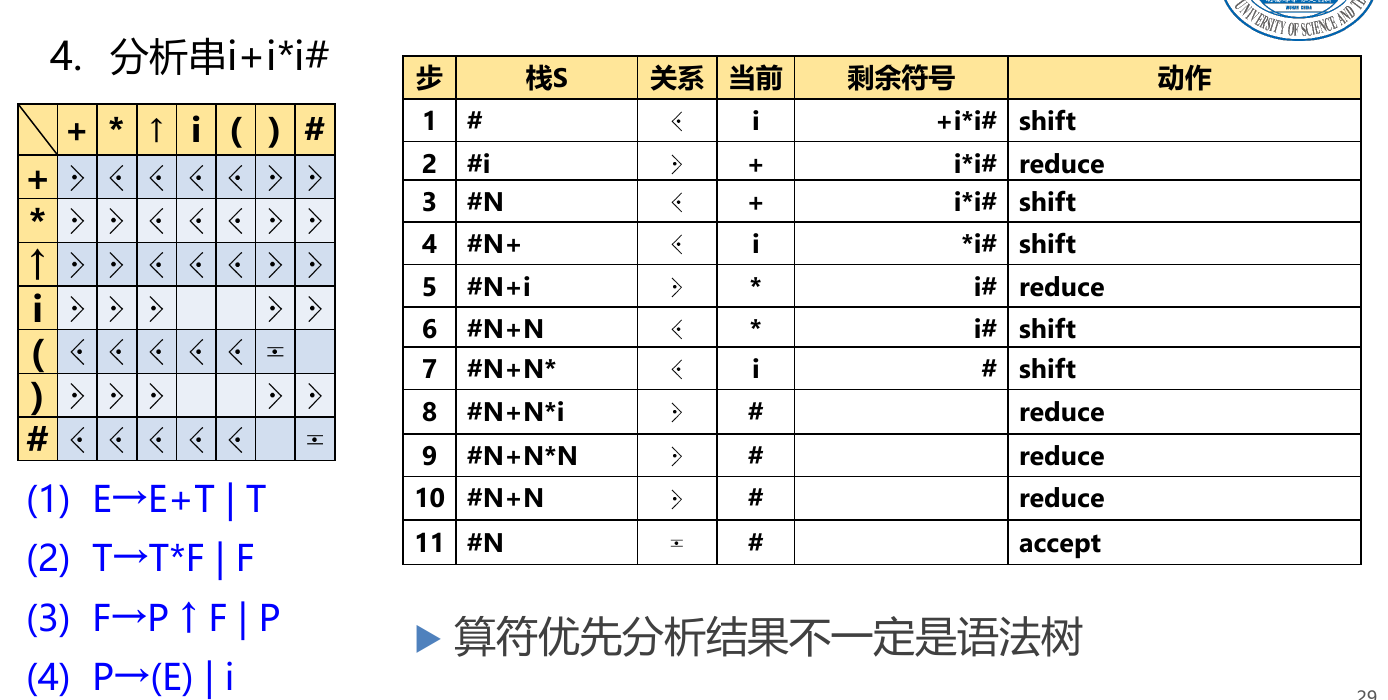
LR 分析
语法分析。本章要对着ppt仔仔细细研究。
LR分析概述
LR(k):L(Left to right parsing), R(right-most derivation in reverse), K(look ahead k token(s))
总控程序、分析栈和分析表三个组成部分,移进-规约法。

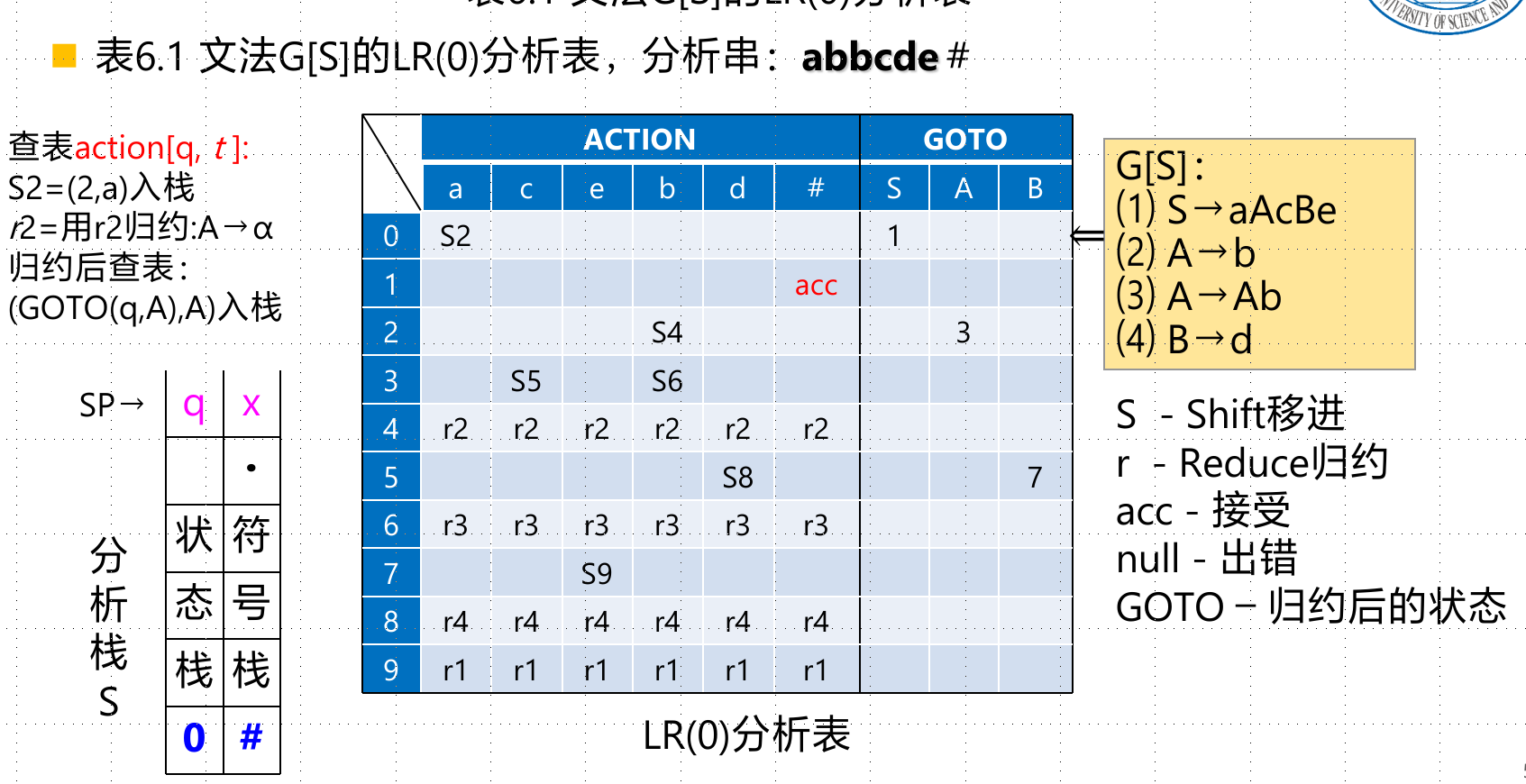
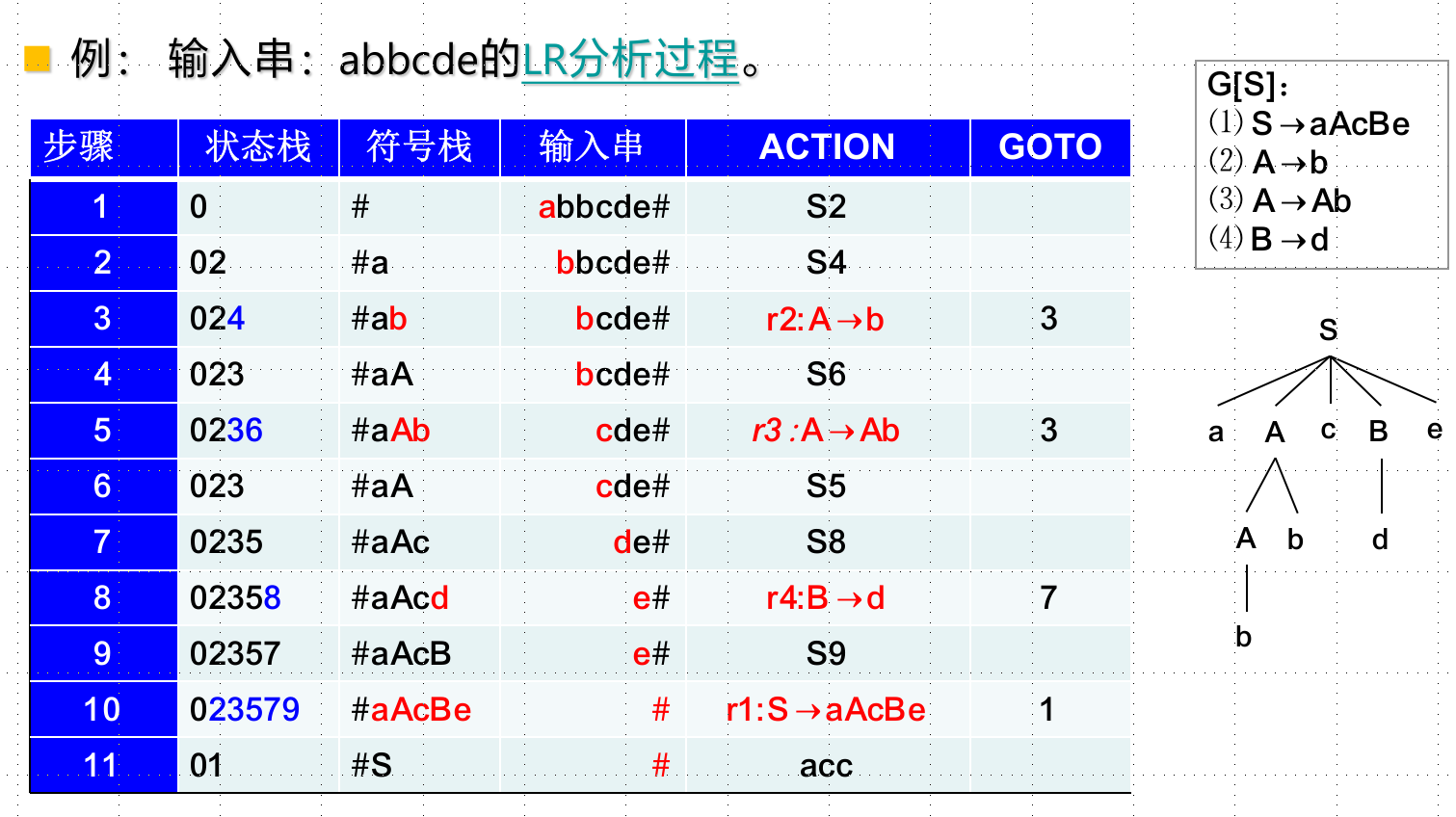
总之,状态栈和符号栈要同进同出。
LR(0)分析
活前缀和可归前缀
简单地说,先找到句柄(最左直接短语),然后活前缀是从符号串最左端到句柄最右端,这一条串的所有前缀。可归前缀是从符号串最左端到句柄最右端这一条串。

识别活前缀DFA
技术线路是根据文法G,构造识别活前缀NFA M。之后通过子集法,将NFA M确定化,得到识别活前缀DFA M′。
- 添加一条$S’\rightarrow S$规则,S’作为起始符,用来给最后转移到接收态。
- S→aAcBe这样的,画状态,最后一个节点标上规则的序号并为可接收态,每个非终结符边前面的状态要通过$\epsilon$转移到相应的规则上面
- 确定化nfa,得到dfa,按照标注的规则转移
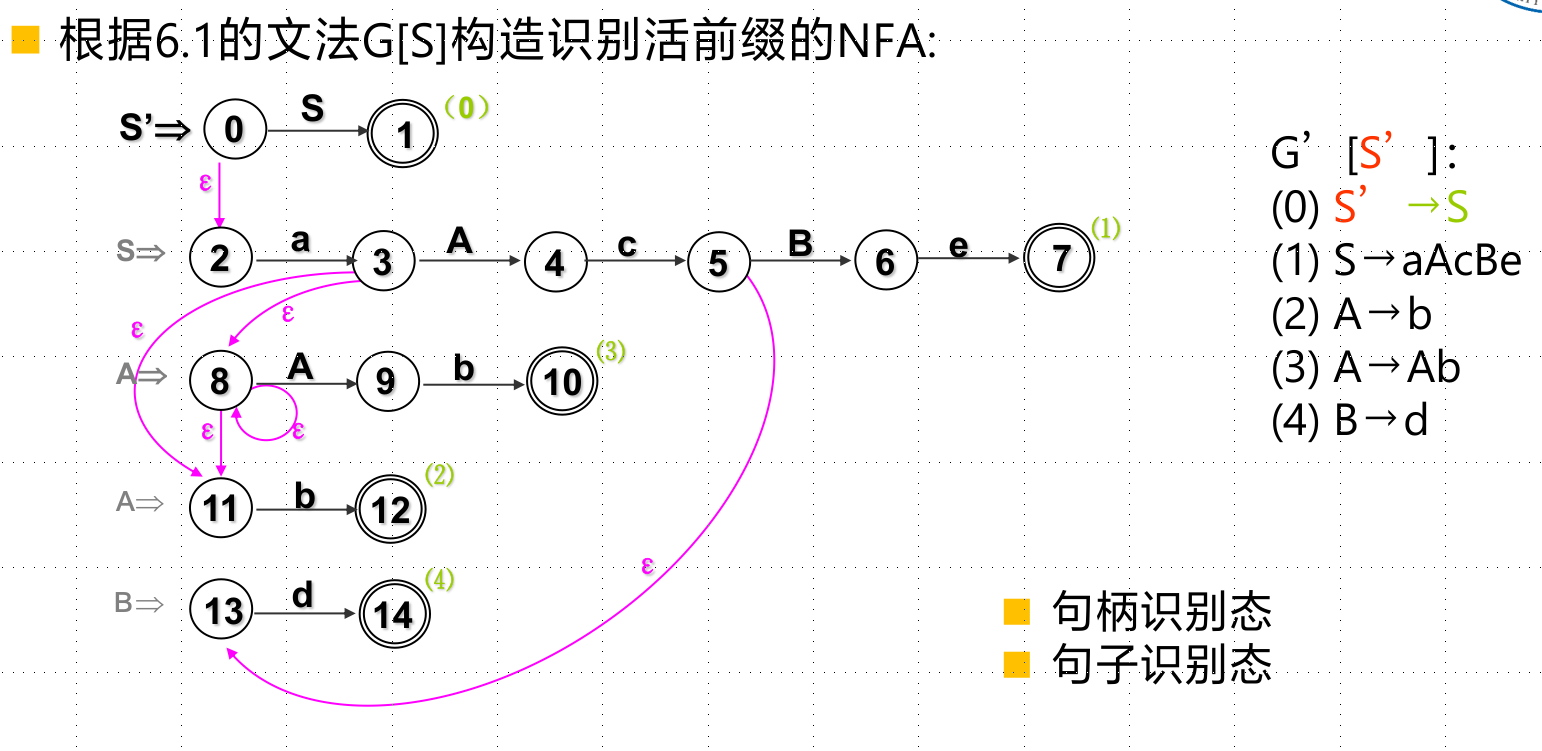
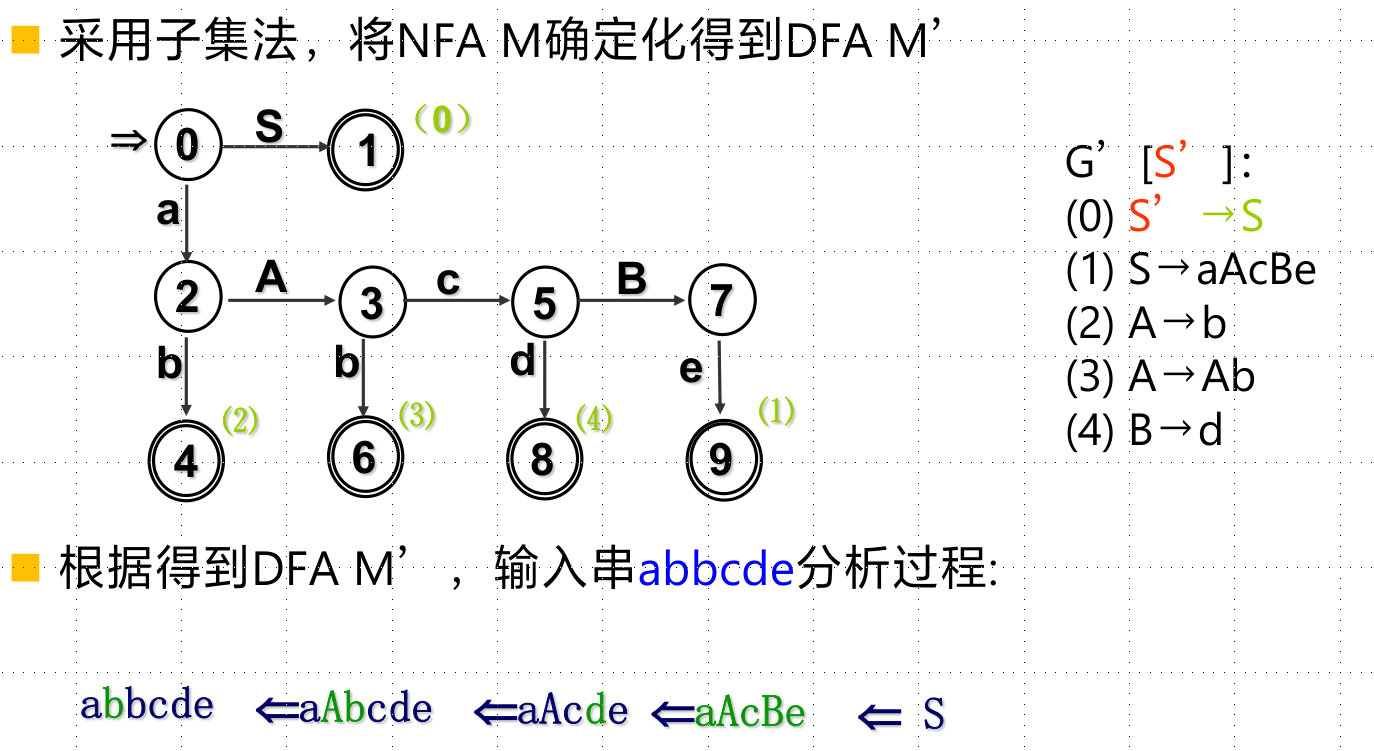
构造LR(0)项目集规范族
首先是给状态取一个规范的名称
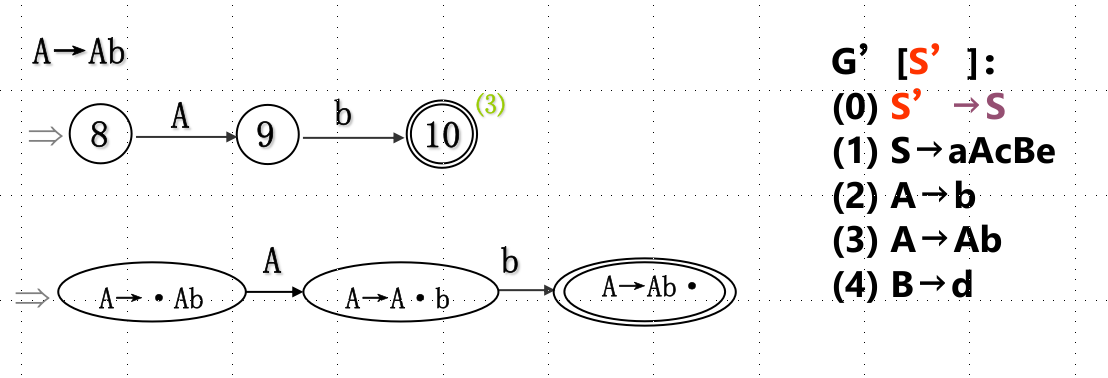
这样的话,可以通过上面的方法构造识别活前缀的dfa,也可以使用LR(0)项目集(规范族)直接构造识别活前缀的DFA。

设I是文法G的LR(0)项目子集,则MOVE(I,X)定义如下:MOVE(I,X) = {A→αX·β︱A→α·Xβ∈I}。move就相当于把点往后挪了一格。
I的闭包就是它和第一个非终结符的规则的集合:

最终构造DFA方法(仔细研读):

文法G的识别活前缀DFA M的状态集称为文法G的LR(0)项目集规范族。
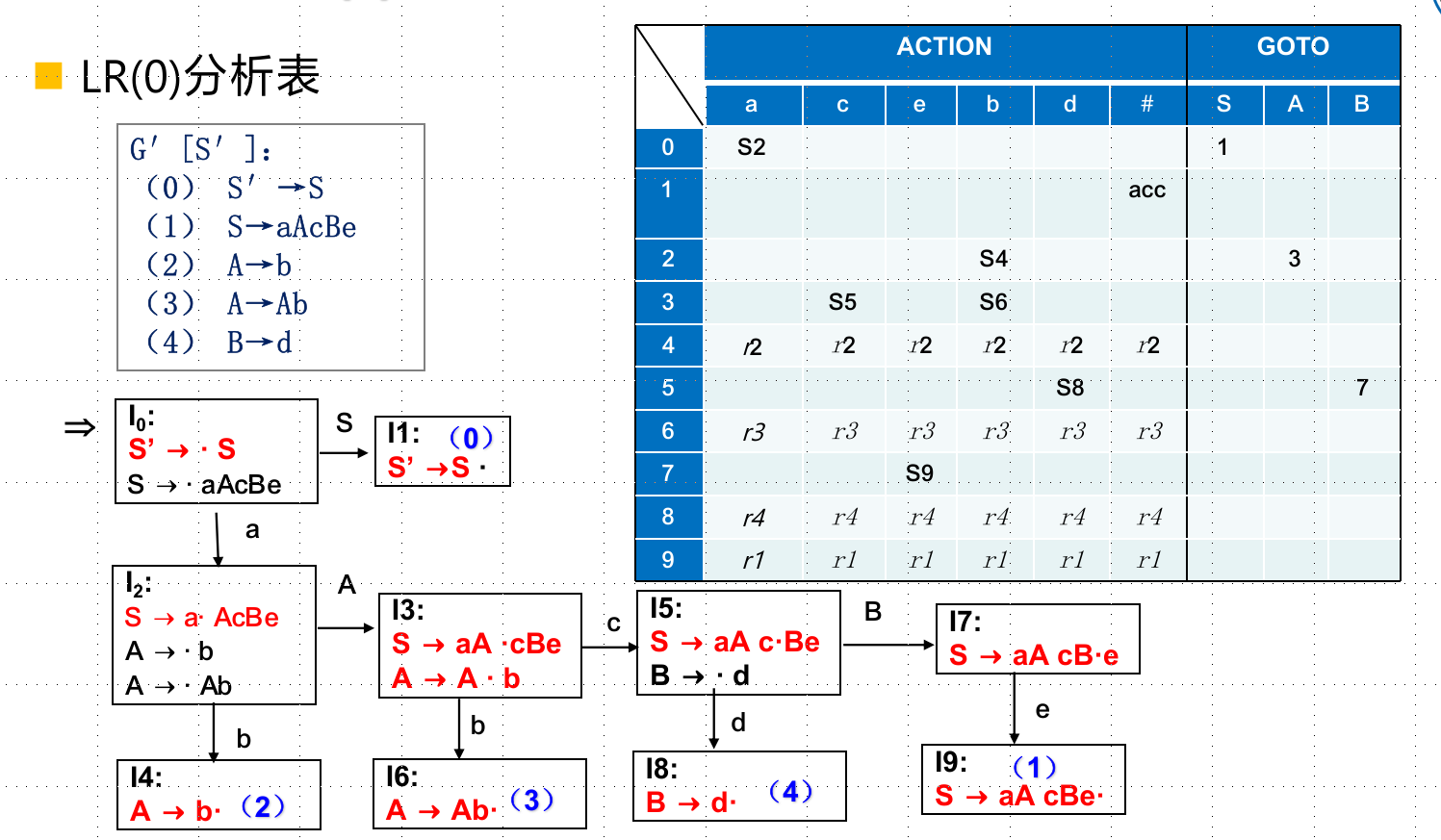
LR(0)分析表的构造

表见上。总之,有一个状态$i$(对应项目集规范族$I_i$)
- 非终结符转移到$j$,填action为j
- $I_i$是不含规约项目的,那么通过终结符转移到j,填action为$S_j$
- $I_i$是含规约项目的,那么全行都是对应的的$r_x$
- 状态1通常是$S’\rightarrow S$,那么action[1,S]为accept。
移进-归约冲突: 项目集中同时出现移进和归约项目:A→α•aβ,B→γ•
归约-归约冲突:项目集中同时出现多个归约项目:A→α•,B→β•
如果文法G的LR(0)项目集规范族不存在移进-归约冲突或归约-归约冲突的项目集,则文法G称为LR(0)文法。可采用LR(0)分析法、无二义性的。分析表ACTION表中每格仅会是移进、归约和报错3种动作之一。
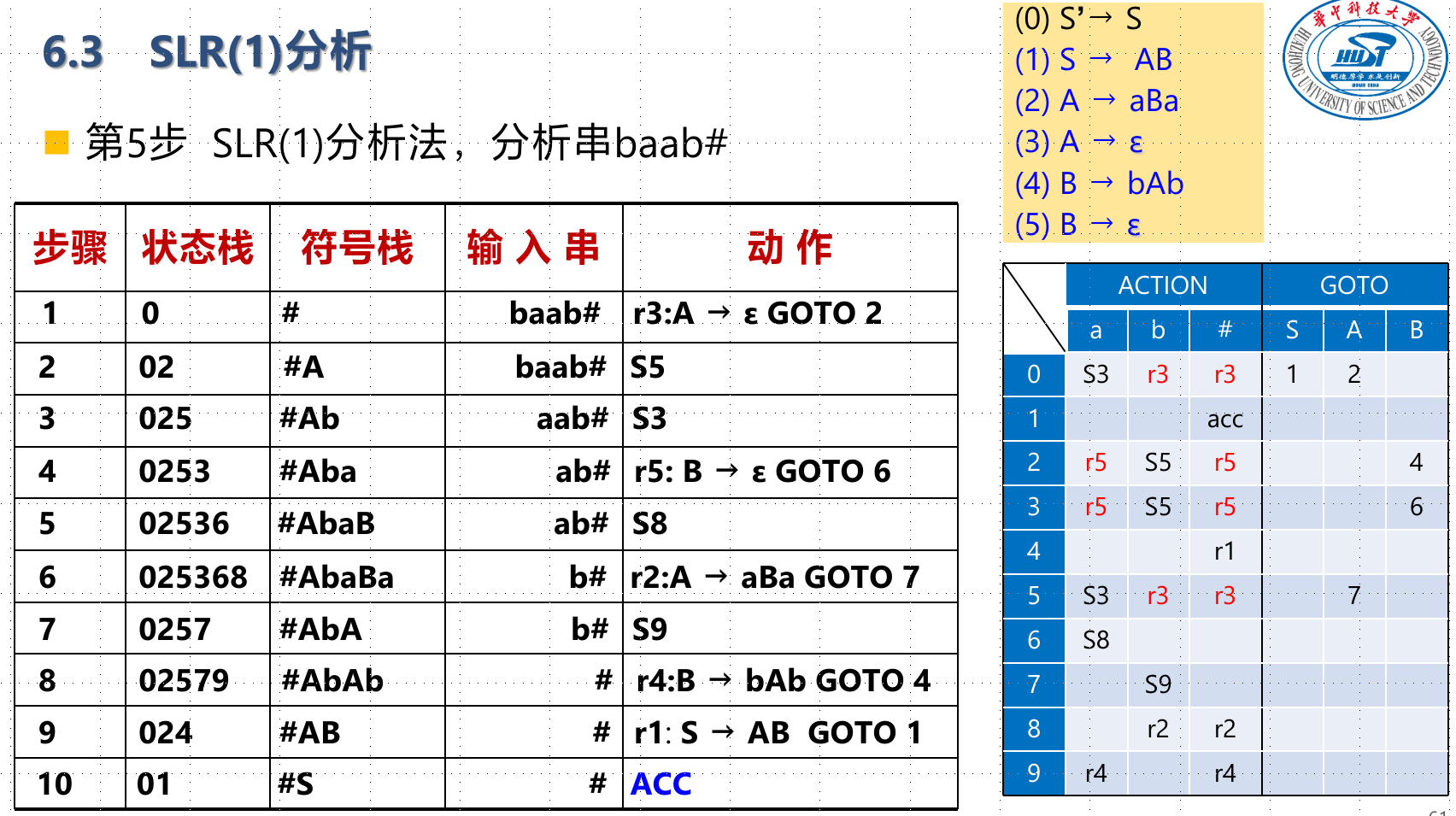
SLR(1)分析
LL(1)的痛苦是解决不了移进-规约冲突和规约-规约冲突问题。
不是LR(0)文法时,可以采用简单地向后看1个输入符号的方法,解决移进-归约冲突或归约-归约冲突。

它的构造法和LR(1)的很类似,除了$I_i$是含规约项目的时候,**不再是简单地把全行都搞成对应的$r_x$**,而是$\forall a\in FOLLOW(A), action[i,a]=r_i$。也就是说得在follow集合里头。

SLR(1)文法,是无二义性的;LR(0)文法,一定也是SLR(1)文法

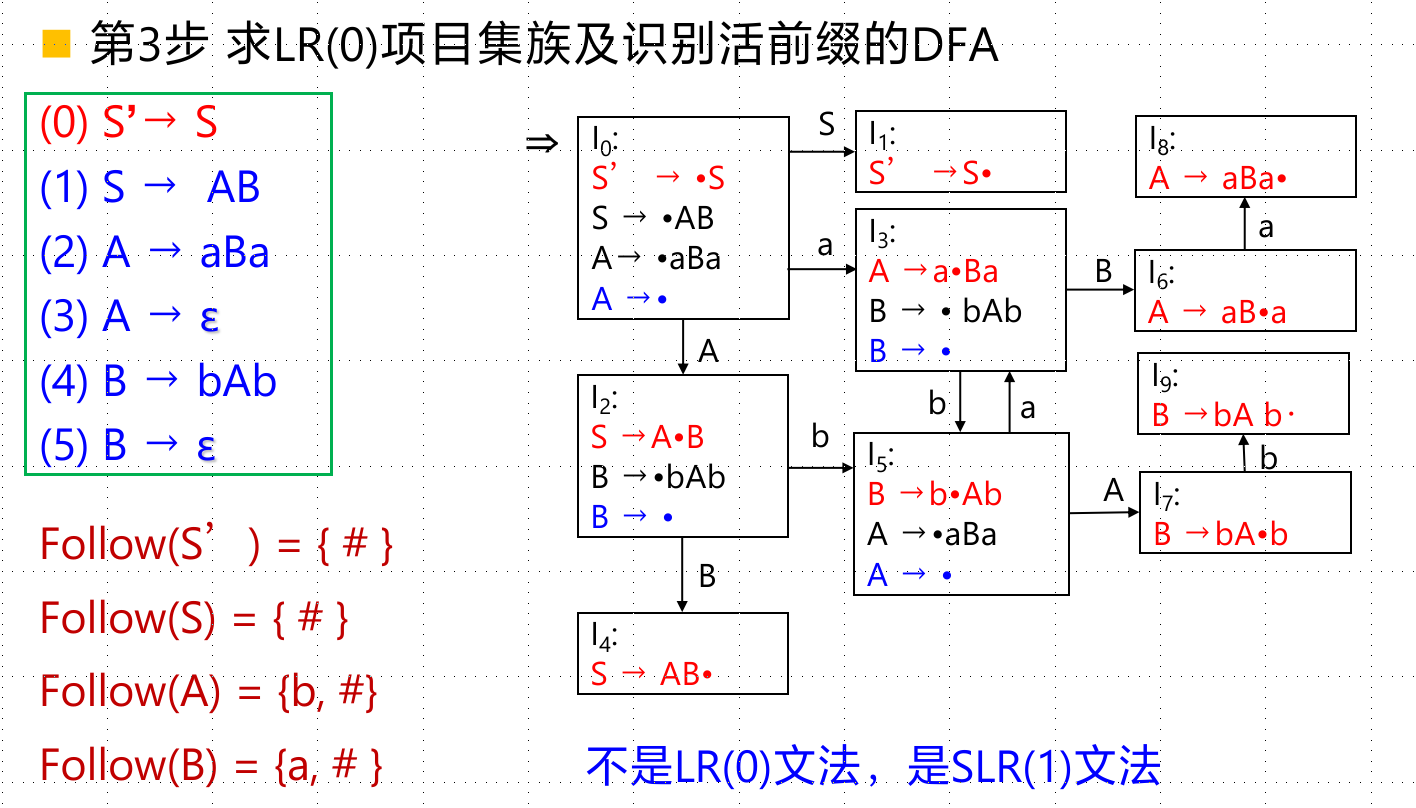
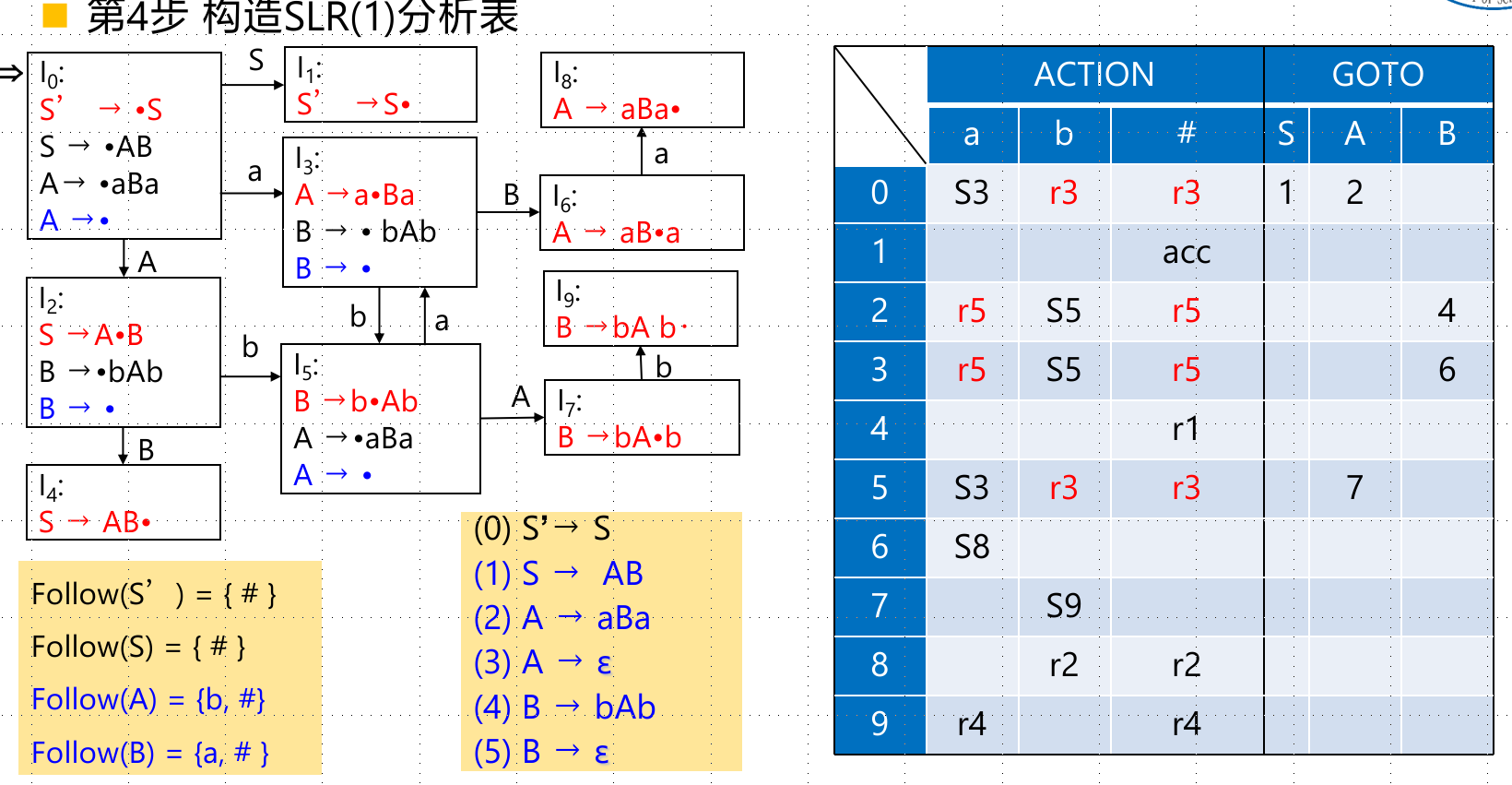
LR(1)分析
b∈FOLLOW(A)只是归约α的一个必要条件,而非充分条件
把First(β)作为产生式作为B→γ归约时向前查看的符号集合,代替SLR(1)分析法中的Follow(B)
并将向前搜索符号集也放在LR(0)项目的后面:[A→α•β, a], a称为向前搜索符(展望符) - LR(1)项目
LR(1)项目中LR(0)项目部分称为LR(1)项目的心。
同心的LR(1)项目简记为 [LR(0)项目,搜索符1︱搜索符2︱···︱搜索符m]。
“搜索符1︱搜索符2︱···︱搜索符m”称为搜索集。
形如[A→α•, a]的项表示仅在下一个输入符号等于a时才可以按照A→α 进行归约;
这样的a的集合总是FOLLOW(A)的子集,通常是真子集
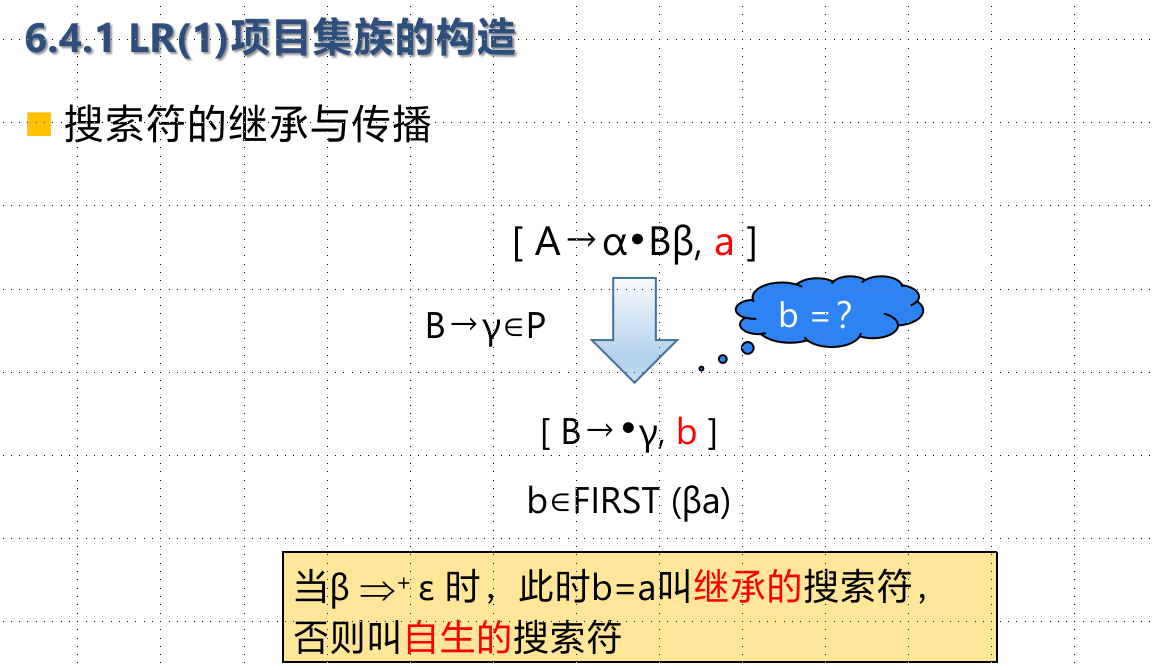

就是非终结符的后头和后继符都那啥



LALR(1)分析
如果采用同心项目集合并方法,进行合并后的文法G的LR(1)项目集规范族,没有LR(1)项目冲突,则称文法G为LALR(1)文法。
合并同心集时产生移进-规约、归约-归约冲突, 就不是LALR(1)文法。
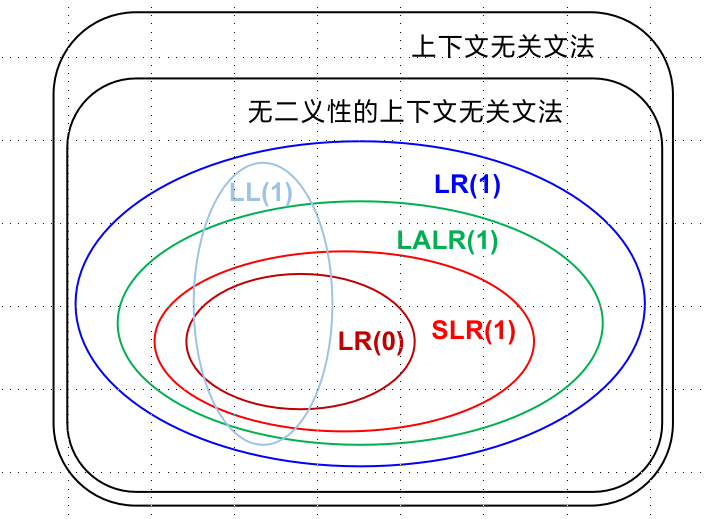
任何一个二义性文法都不是LR的
语法制导的语义计算
基于属性文法的语义计算
属性文法
综合属性:
- 自下而上传递信息
- 语法规则:产生式左部符号的综合属性由产生式右部符号的属性计算得出
- 语法树:父节点的综合属性由子结点的属性和父结点自身的属性计算得出
终结符的综合属性值是由词法分析器提供的词法值,因此在属性文法中没有计算终结符属性值的语义规则
继承属性:
自上而下传递信息
语法规则:根据右部候选式中的符号的属性和左部符号的属性计算右部候选式中的符号的继承属性
语法树:根据父结点和兄长节点的属性计算子结点的继承属性
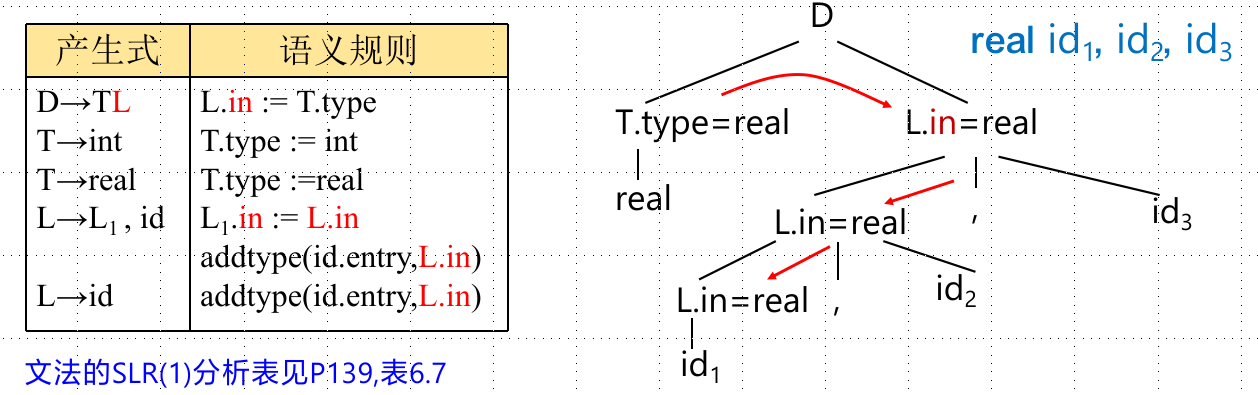
产生式右部符号的继承属性和产生式左部符号的综合属性由本产生式提供计算规则。且规则中只能使用本产生式中文法符号的属性。
产生式左部符号的继承属性和产生式右部符号的综合属性的计算规则不由本产生式提供,而是根据其它产生式的语义规则来计算。
带注释的语法树(仅含综合属性):仅使用综合属性的属性文法称S-属性文法
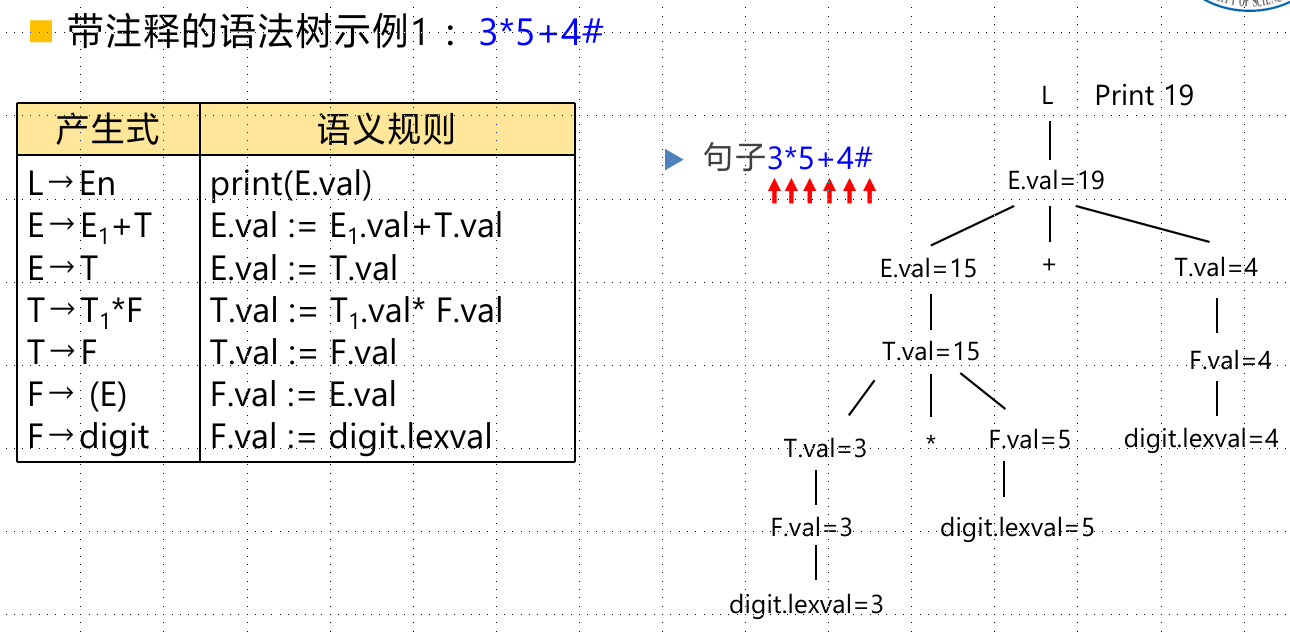
带注释的语法树(含继承属性):先构造语法树,再计算属性。
语义计算
属性依赖:

如果属性X.a的值依赖于属性Y.b的值,则依赖图中有一条从Y.b的结点指向X.a的结点的有向边
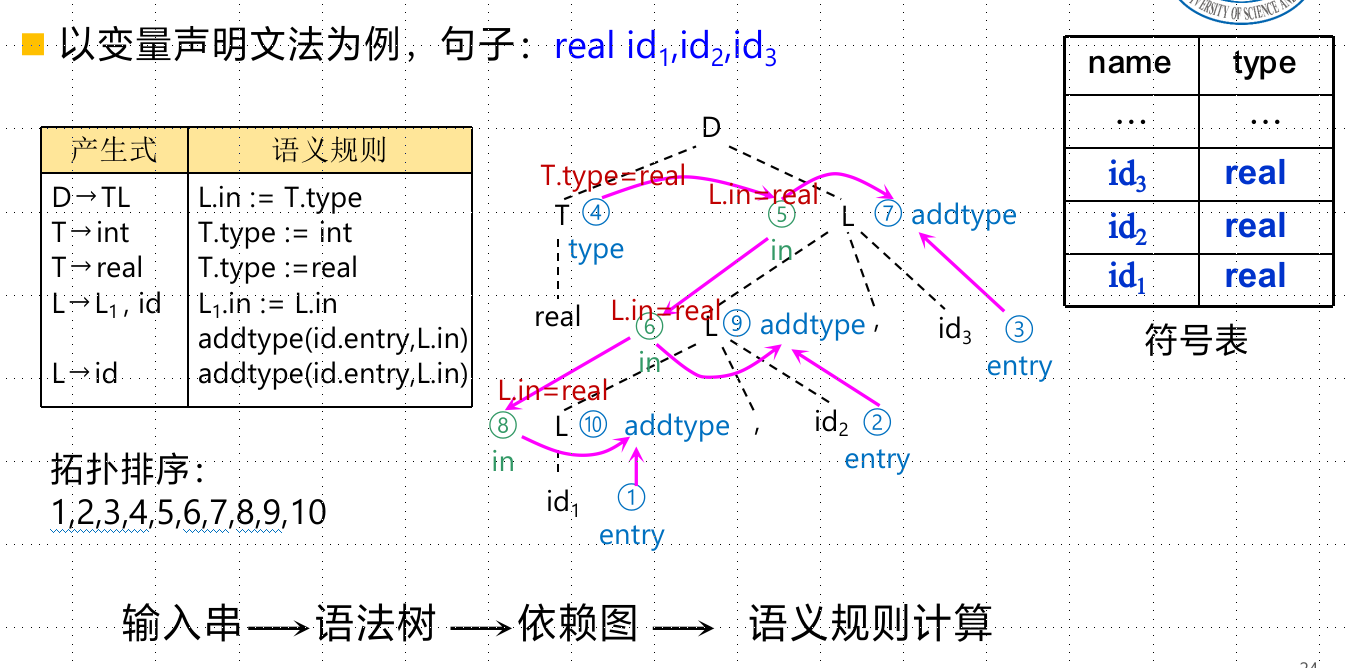
树遍历算法:
1 | While 还有未被计算的属性 do |
一遍扫描法:
在语法分析的同时计算属性值
语义规则被计算的时机
- 自上而下分析,一个产生式匹配输入串成功时
- 自下而上分析,一个产生式被用于进行归约时
S-属性文法和L-属性文法
仅含综合属性的属性文法称为S-属性文法

基于S-属性文法的语义计算
给LR分析栈里头加上一个语义栈

基于L-属性文法的语义计算
上面的树遍历法
基于翻译模式的语义计算
翻译模式
属性文法的语义规则:总是放在产生式的尾部
翻译模式:把语义规则(也称语义动作),用花括号{ }括起来,插入到产生式右部的合适位置上。进一步细化了语义计算的时机。
基于S-翻译模式的语义计算
S-翻译模式:仅涉及到综合属性,通常语义动作集置于产生式右端的末尾。常采用LR的自底向上的分析法,和S属性文法类似。
与S-属性文法类似
- 基础文法是LL(1):自顶向下计算
- 基础文法是LR系:自底向上计算
基于L-翻译模式的自顶向下计算

- 分析程序由一组递归子程序(函数)组成,每个非终结符对应一个子程序
- 如果非终结符有多个产生式,根据当前符号和SELECT集决定用哪个产生式
- 从左到右分析符号串,遇到终结符就匹配,遇到非终结符就调用相应的分析子程序
- 要求基础文法是LL(1)的
基于L-翻译模式的自底向上计算
从翻译模式中删除嵌入在产生式中间的语义动作
继承属性的求值结果以综合属性值存放在语义栈中,对继承属性的访问变成对语义栈中某个综合属性的访问
模拟继承属性的计算

静态语义分析和中间代码生成
静态语义分析
类型表达式:
基本类型是类型表达式
若T是类型表达式,I是整数域 (0..5; 1..10), 则Array(I,T) 也是类型表达式
若T是类型表达式,则pointer(T)是类型表达式
……
中间代码生成
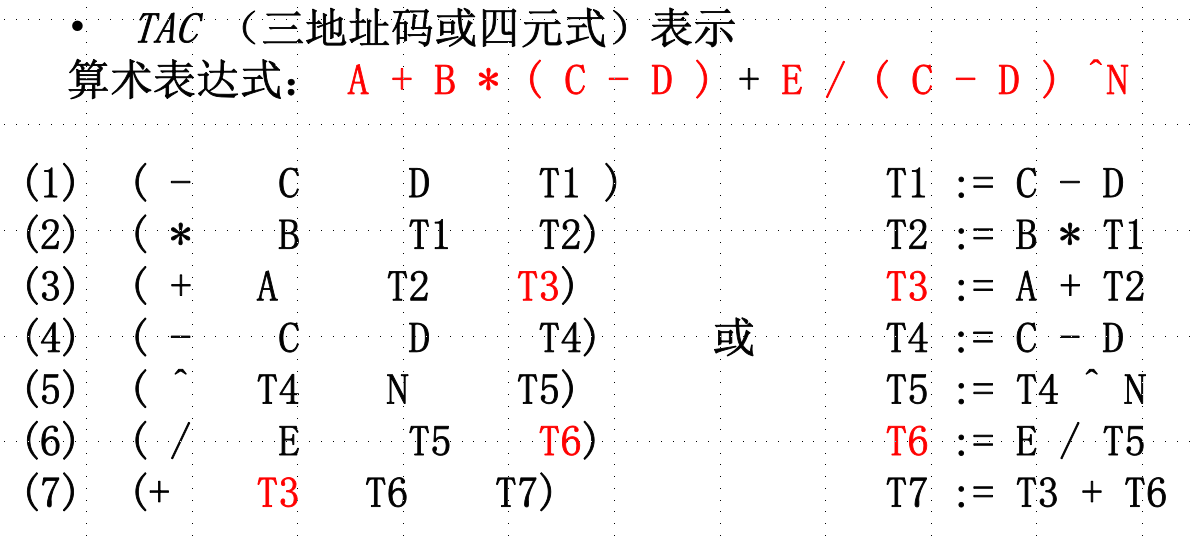
赋值语句和算术表达式的翻译
S -> id := E
语义属性
id.place : id 对应的存储位置
E.place : 用来存放 E 的值的存储单元的地址
E.code : 对E 求值的 TAC 语句序列
S.code : 对应于 S 的 TAC 语句序列
语义函数/过程
gen() : 生成一条 TAC 语句
newtemp() : 在符号表中新建一个从未使用过的名字,
并返回该名字的存储位置
|| 是TAC 语句序列之间的链接运算

说明语句的翻译


bool表达式的翻译

拉链与代码回填(backpatching)



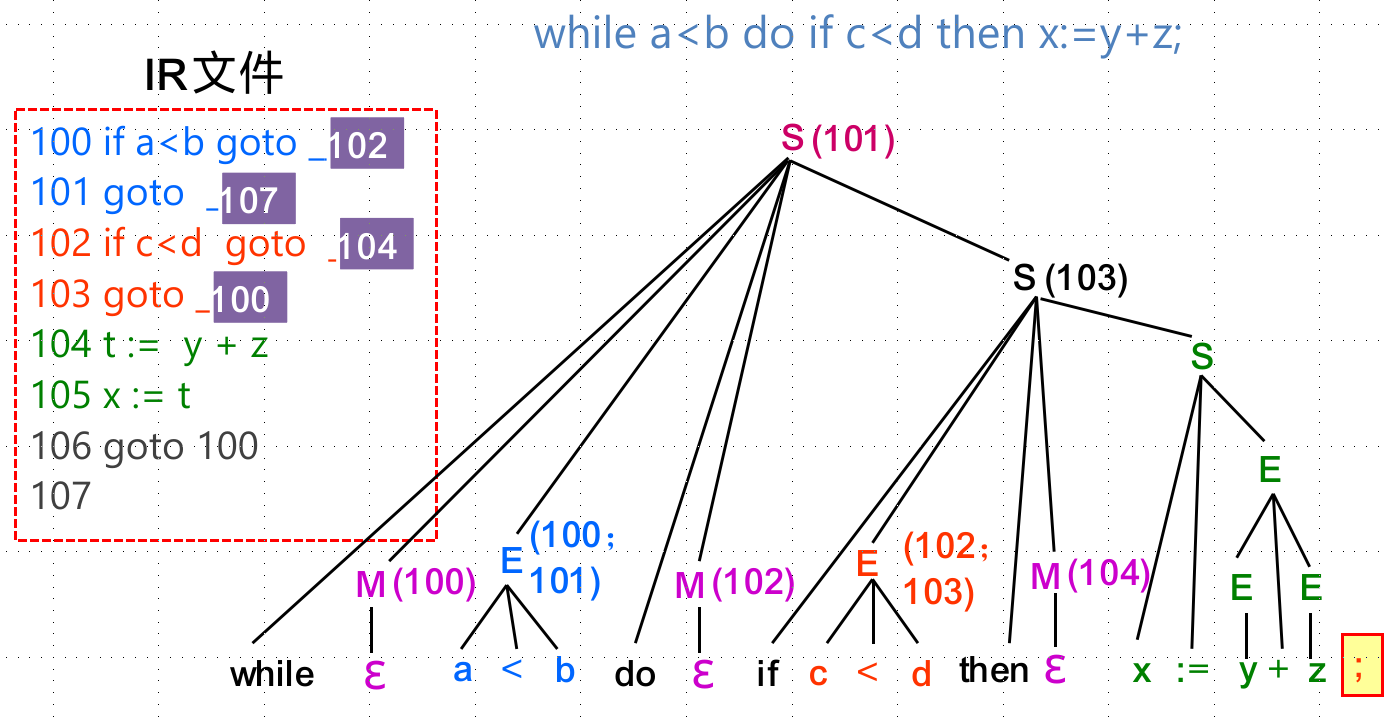
运行时存储组织
运行时存储组织概述

静态存储分配
数据空间仅需要有静态数据区即可。对于所有数据对象,其分配的存储地址都是相对于静态数据区的偏移量,即登记在符号表中数据对象的地址( .place)属性值。
绝对地址 = 静态数据区首址 + 偏移量
栈式存储分配
- 调用子程序时,在栈顶,给子程序分配所需的子程序数据区;
- 子程序返回时,从栈顶,收回分配给子程序所占用存储区。
- 当子程序被递归调用时,同一个子程序可能在数据空间中同时拥有多个子程序数据区,每个数据区对应于同一个子程序的一次执行过程。
对于所有数据对象,其分配的存储地址都是相对于数据对象所在的子程序数据区的偏移量。
栈帧又叫活动记录。
堆式存储分配
略
活动记录(栈帧)
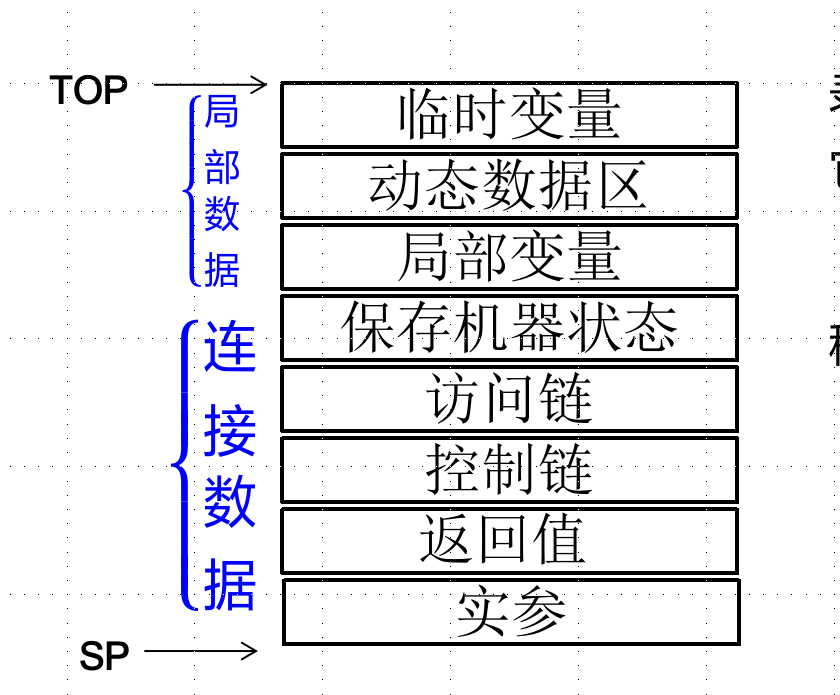
注意:在本题中,int的单元数是1,float的单元数是2!
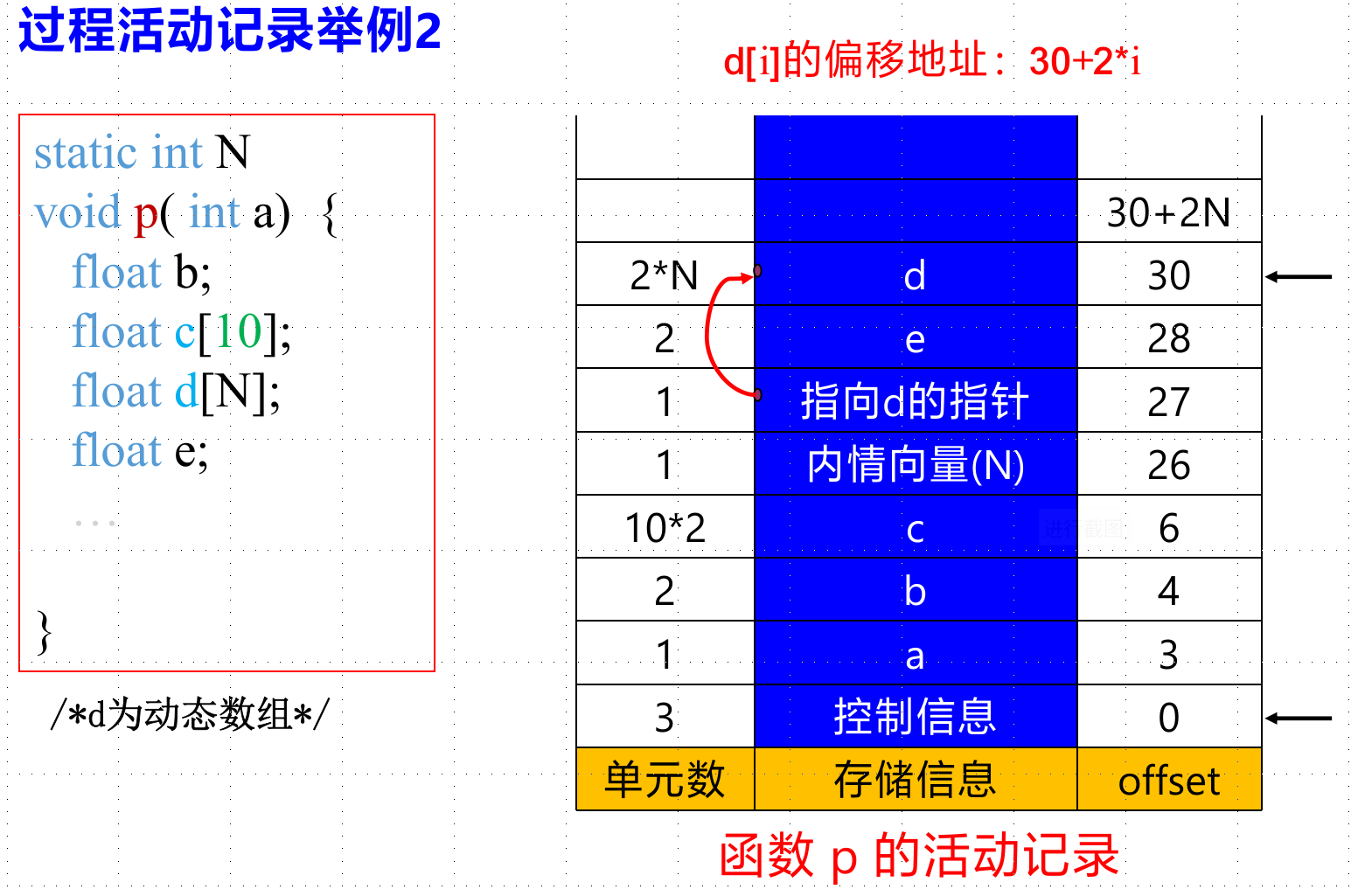
嵌套程序块:太难了,感觉不会考
过程调用
call-by-value :调用过程计算实参的值,将其放于对应的存储空间,被调用过程执行时,就像使用局部变量一样使用这些形式单元

call-by-reference:想想C语言,很直观
代码优化与目标代码生成
优化技术介绍
常量折叠:r2 = 2 * 3 优化为 r2 = 6
常量传播:代入常量
常量传播可能导致分枝判断条件是常量,从而导致分枝的代码不需要执行,这种优化叫做稀疏有条件的常数传播
……略
基本块、流图、循环
基本块
基本块是一个最大的不可分割的、连续的三地址指令序列,这个块中的指令要么全执行,要么全不执行。
基本块的入口:
- 程序的第1条语句;
- (条件/无条件)跳转语句的跳转目标语句;
- 条件跳转语句的下一条语句;
划分基本块的方法如下:
- 依据入口语句定义,确定程序所有的入口语句;
- 对每一个入口语句,确定对应的基本块。这些基本块是由入口语句向后直到
- 转移语句(包括该语句在内);
- 或到停止语句;
- 或到下一个入口语句(不包括该语句)之间的代码段。
- 凡不属于任何一个基本块的语句都是无用语句,将其全部删除。
流图
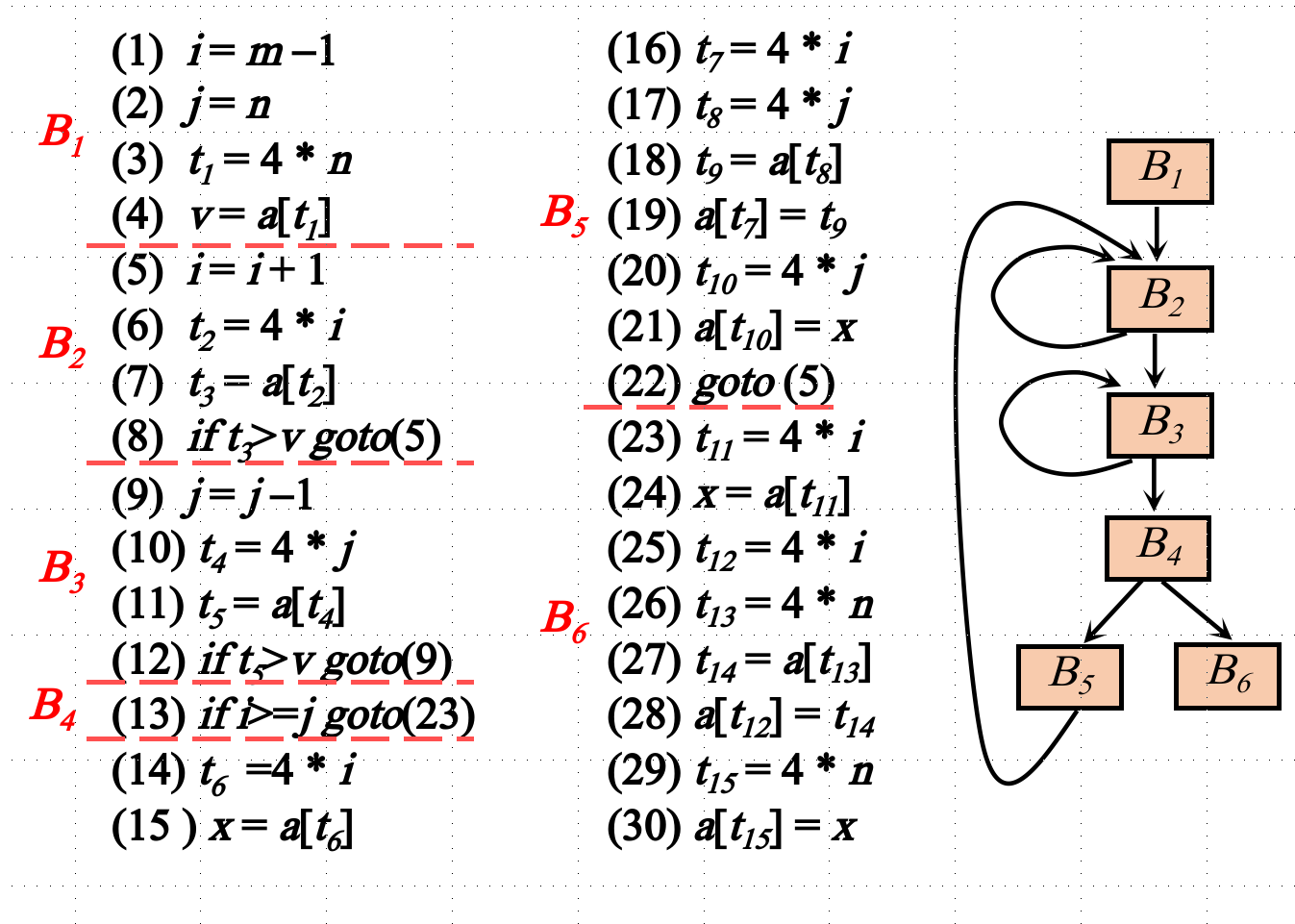
一般把基本块划分和图画到一块(图里头放基本块)
常用优化方法
删除公共子表达式(CSE):如果表达式x op y先前已被计算过,并且从先前的计算到现在,x op y中变量的值没有改变,那么x op y的这次出现就称为公共子表达式
cse可以是基本块内的,也可以是其他基本块的,叫做全局公共子表达式。
删除全局公共子表达式的时候要非常谨慎,因为很有可能在别的块改了值!
删除无用代码:常用的公共子表达式消除算法会引入一些形如x = y的赋值语句,在其之后尽可能地用y代替x,然后就能给删除无用代码带来机会
常量合并:前面讲了
代码移动:不管循环执行多少次都得到相同结果的表达式,在进入循环之前就对它们求值
强度削弱:用较快的操作代替较慢的操作,如用加代替乘
循环:
在程序流图G中,对于任意一个结点序列α,如果在结点序列之外存在一个结点指向结点序列中的结点V,或者结点序列中的结点V是程序首结点,则称结点V 为结点序列α的入口结点。

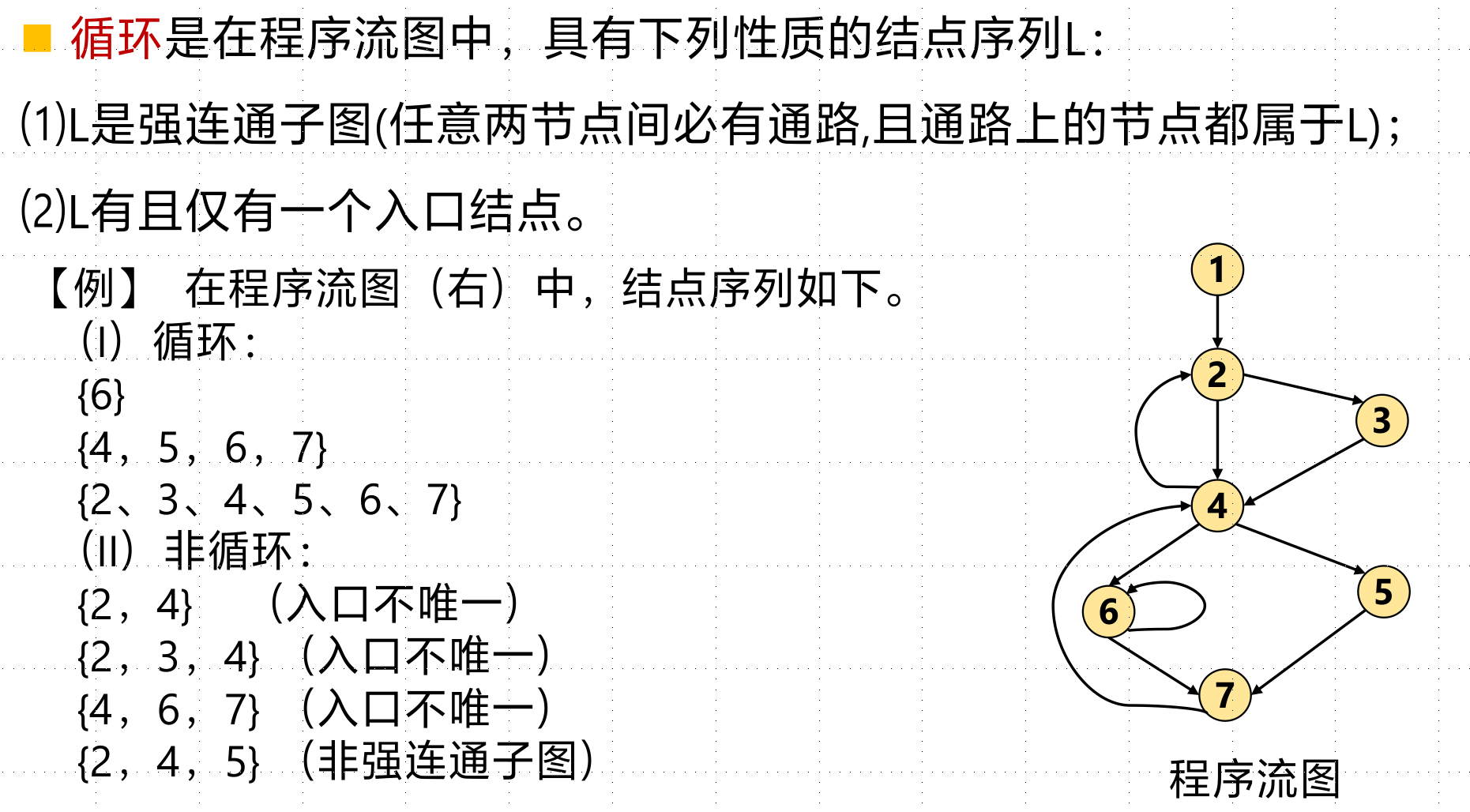
求循环:我感觉这玩意考不了
代码优化技术
窥孔优化
删除冗余的存(store)或取(load)操作
局部优化(重点)
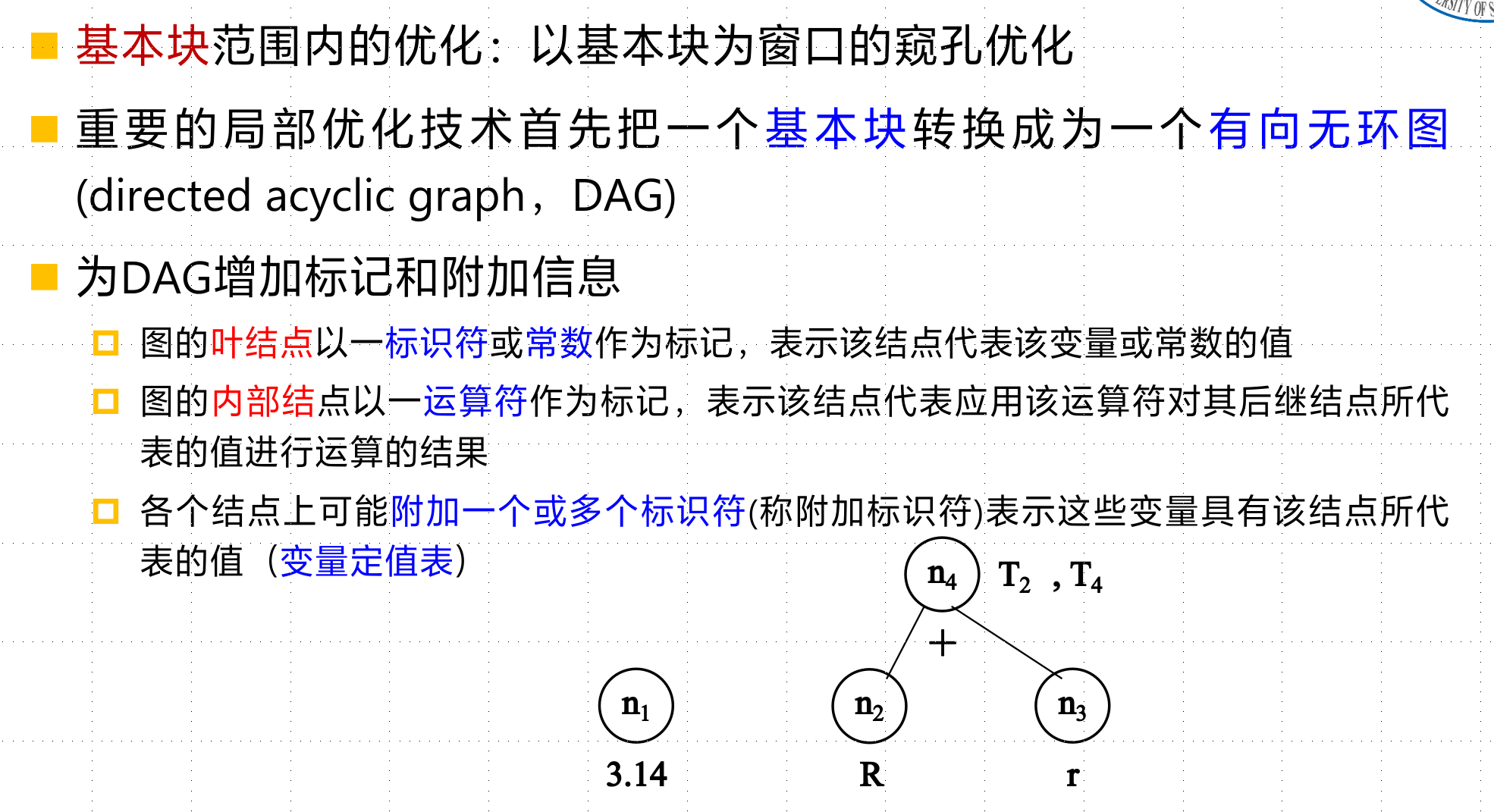
对基本块中每一条四元式代码,依次构造对应的DAG图,最后基本块中所有四元式构造出来DAG连成整个基本块的DAG,
- 准备操作数的结点
- 常量合并
- 常量传播
- 复制传播
- 删除公共子表达式
- 删除无用赋值(死代码)
循环优化
对循环中的代码,可以实行
- 代码外提
- 归纳变量强度消弱
- 删除归纳变量(变换循环控制条件)
- 循环展开
- 循环合并
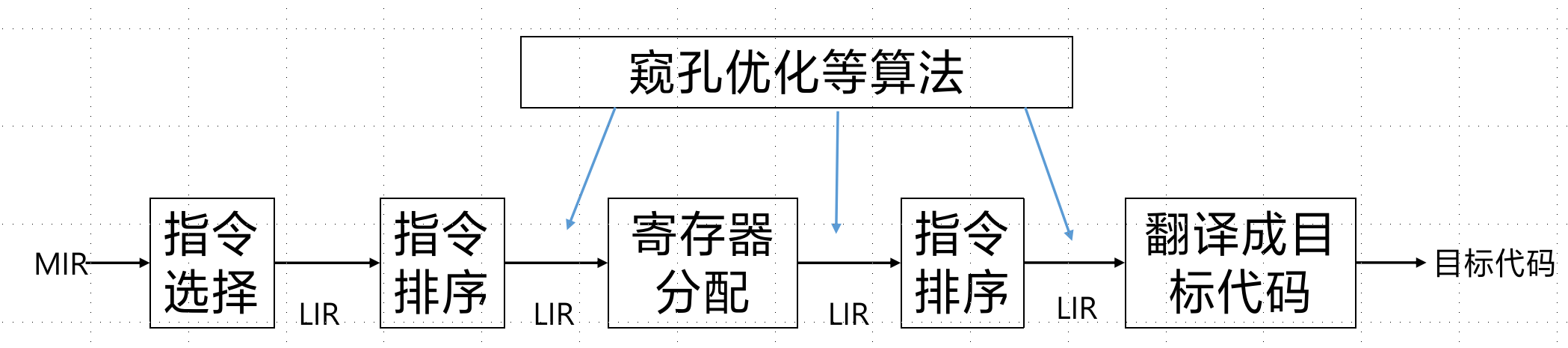
目标代码生成技术